읽기 전
- 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
- 개인적으로 사용해보면서 배운 점을 정리한 글입니다.
프림 알고리즘(Prim's Algorithm)이란?
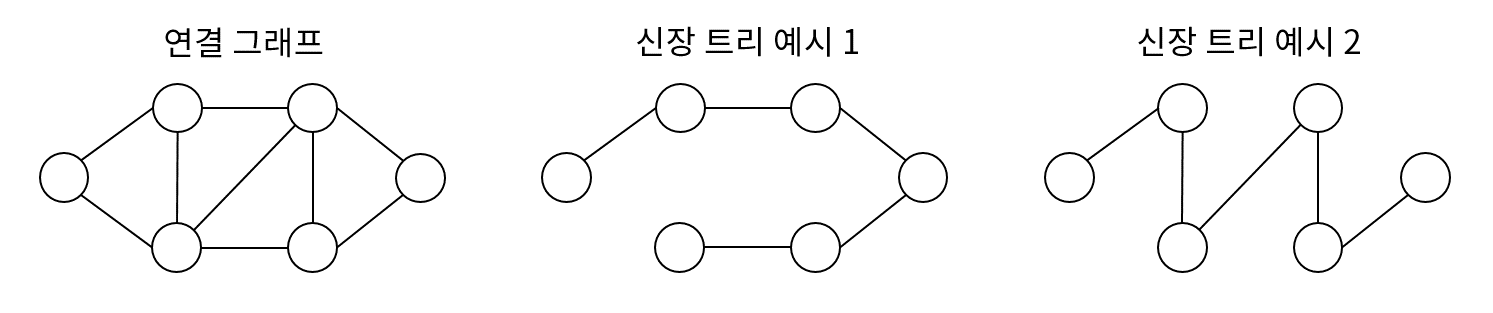
최소 신장 트리(Minimum Spanning Tree) 구현에 사용되는 알고리즘으로 시작 정점에서 정점을 추가해가며 단계적으로 트리를 확장하는 기법이다.
프림 알고리즘의 동작
프림 알고리즘은 매 순간 최선의 조건을 선택하는 그리디 알고리즘을 바탕에 둔다. 즉, 탐색 정점에 대해 연결된 인접 정점들 중 비용이 가장 적은 간선으로 연결된 정점을 선택한다.
- 시작 단계는 시작 노드만이 MST 집합에 속한다.
- 트리 집합에 속한 정점들과 인접한 정점들 중 가장 낮은 가중치의 간선과 연결된 정점에 대해 간선과 정점을 MST 트리 집합에 넣는다. (사이클을 막기 위해 연결된 정점이 이미 트리가 속한다면 그 다음 순서를 넣는다.)
- 2번 과정을 MST 집합의 원소 개수가 그래프의 정점의 개수가 될 때까지 반복한다. (간선의 가중치를 더해서 최소 신장 트리 비용 산출)
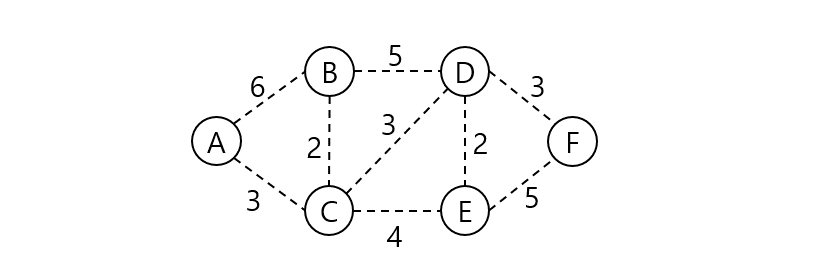
위 그래프의 최소 신장 트리를 프림 알고리즘으로 구해보자. 시작 정점은 A라 한다.
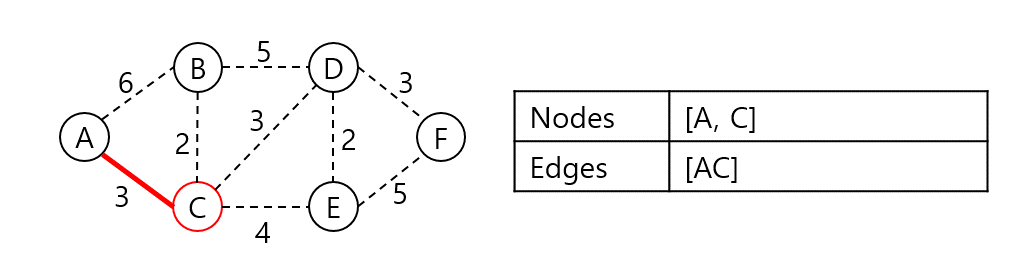
A와 인접한 노드 B, C 중 C가 가장 가중치가 낮은 간선으로 연결되어 있으니 C를 집합에 넣고 비용에 AC 가중치를 더한다.
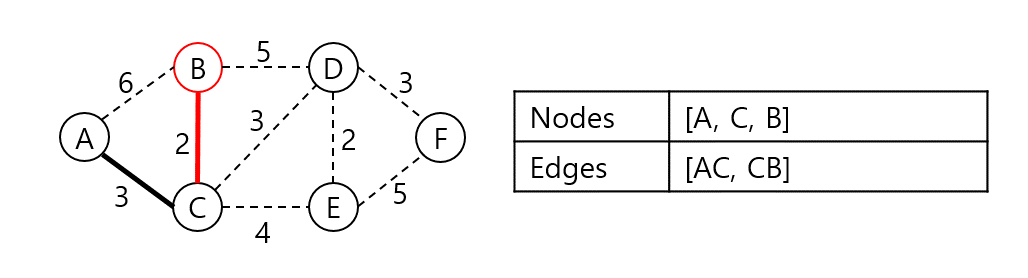
AC와 인접한 노드들 중 가장 낮은 가중치로 연결된 정점은 B다. 집합에 B를 넣고 CB 가중치를 더한다.
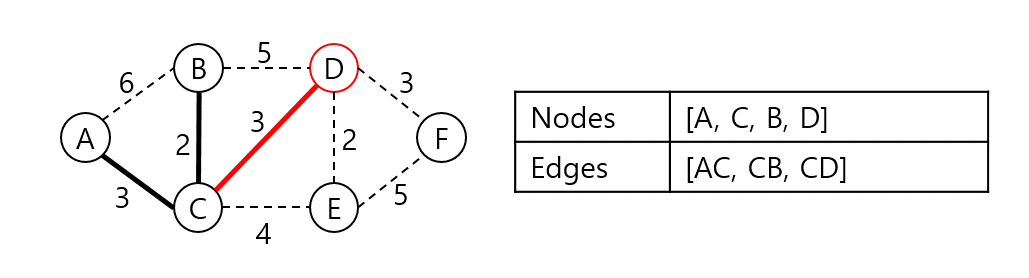
A, C, B와 인접한 노드들 중 가장 낮은 가중치로 연결된 정점은 D다. 집합에 D를 넣고 CD 가중치를 더한다.
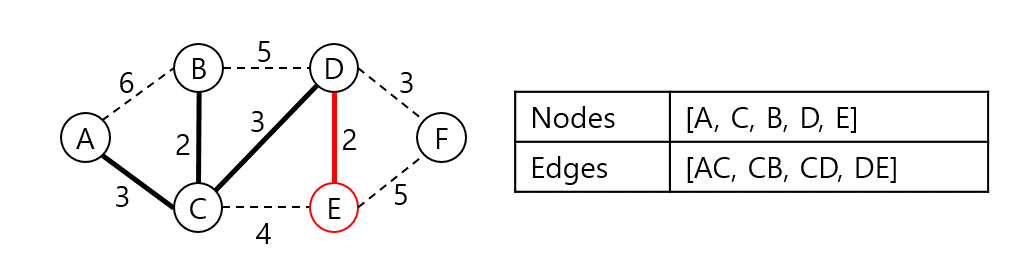
A, C, B, D와 인접한 노드들 중 가장 낮은 가중치로 연결된 정점은 E다. 집합에 E를 넣고 DE 가중치를 더한다.
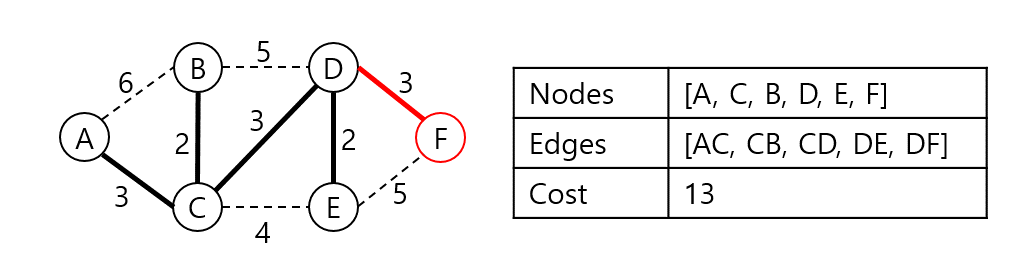
A, C, B, D, E와 인접한 노드들 중 가장 낮은 가중치로 연결된 정점 F를 집합에 넣고 DF 가중치를 더한다. 트리의 집합에 속한 원소의 개수가 N이 되었으므로 탐색을 중단한다. 탐색 결과 최소 신장 트리 구축의 비용은 13으로 확인되었다.
프림 알고리즘의 구현
동작 과정을 살펴본 결과 인접 정점들 중 가중치가 가장 낮은 정점을 찾는 과정이 시간복잡도를 결정할 것으로 보인다. 그렇다면 집합 내 정점들을 순회하면서 우선순위 큐에 삽입한 뒤 pop하여 구현하면 도움이 되겠다.
python 코드
from collections import defaultdict
import heapq
def mst():
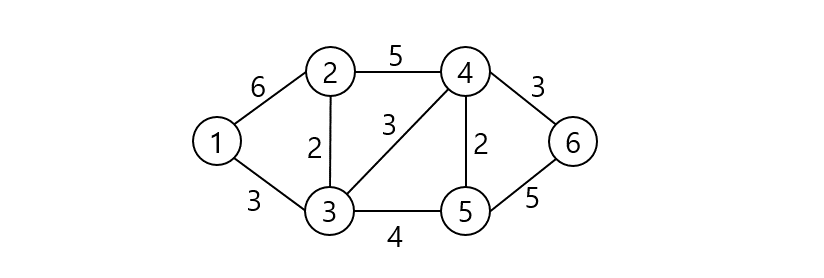
V, E = 6, 9
edges = [[1, 2, 6], [1, 3, 3], [2, 3, 2], [2, 4, 5],
[3, 4, 3], [3, 5, 4], [4, 5, 2], [4, 6, 3], [5, 6, 5]]
graph = defaultdict(list)
for srt, dst, weight in edges:
graph[srt].append((dst, weight))
graph[dst].append((srt, weight))
mst_graph = [[0] * V for _ in range(V)]
mst_nodes = [-1 for _ in range(V)]
visited = [True for _ in range(V)]
q = [(0, 1, 1)]
while q:
cost, node, prev = heapq.heappop(q)
if visited[node - 1] is False:
continue
visited[node - 1] = False
mst_graph[node - 1][prev - 1] = 1
mst_graph[prev - 1][node - 1] = 1
mst_nodes[node - 1] = cost
for dst, weight in graph[node]:
if visited[dst - 1] is True:
heapq.heappush(q, (weight, dst, node))
print(f'MST cost is {sum(mst_nodes)}')
mst_graph[0][0] = 1
for row in mst_graph:
print(*row)
mst()
프림 알고리즘 시간복잡도
모든 노드에 대해 탐색을 진행하므로 $O(V)$이다. 그리고 우선순위 큐를 사용하여 매 노드마다 최소 간선을 찾는 시간은 $O(log\ V)$이다. 따라서 탐색과정에는 $O(Vlog\ V)$가 소요된다. 그리고 각 노드의 인접 간선을 찾는 시간은 모든 노드의 차수와 같으므로 $O(\sum_{v=1}^V degree(v))$$=O(2E)$$=O(E)$다. 그리고 각 간선에 대해 힙에 넣는 과정이 $O(log\ V)$가 되어 우선순위 큐 구성에 $O(Elog\ V)$가 소요된다. 따라서, $O(Vlog\ V + Elog\ V)$로 $O(Elog\ V)$가 되겠다.($\because$ E가 일반적으로 V보다 크기 때문)
만약 우선순위 큐가 아니라 배열로 구현한다면 각 정점에 최소 간선을 갖는 정점 탐색을 매번 정점마다 수행하므로 $O(|V|^2)$가 되고 탐색 결과를 기반으로 각 정점의 최소 비용 연결 정점 탐색에는 $O(1)$이 소요된다. 따라서 시간복잡도는 $O(V^2)$이다.
관련 링크
'Algorithms > Algorithm' 카테고리의 다른 글
| 크루스칼 알고리즘(Kruskal's Algorithm) (0) | 2021.08.02 |
|---|---|
| 플로이드-워셜 알고리즘(Floyd-Warshall Algorithm) (0) | 2021.08.01 |
| 벨만-포드 알고리즘(Bellman-Ford Algorithm) (0) | 2021.08.01 |
| 다이나믹 프로그래밍(Dynamic Programming, 동적 계획법) (0) | 2021.07.23 |
| 순열, 조합 순서쌍 구현 (0) | 2021.07.22 |