읽기 전
- 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
- 개인적으로 배운 점을 정리한 글입니다.
문제 링크
문제 풀이
LCS(Longest Common Subsequences) 문제는 두 문자열이 주어졌을 때 모두의 부분 문자열이 되는 문자열 중 가장 긴 문자열을 찾는 문제이다. 경험해보지 않으면 풀기가 상당히 까다로워 정리하고자 한다.
예시에 나와있듯이 ACAYKP와 CAPCAK의 LCS를 찾는다고 해보자. 우선 2차월 배열을 생성하고 0으로 초기화한다.
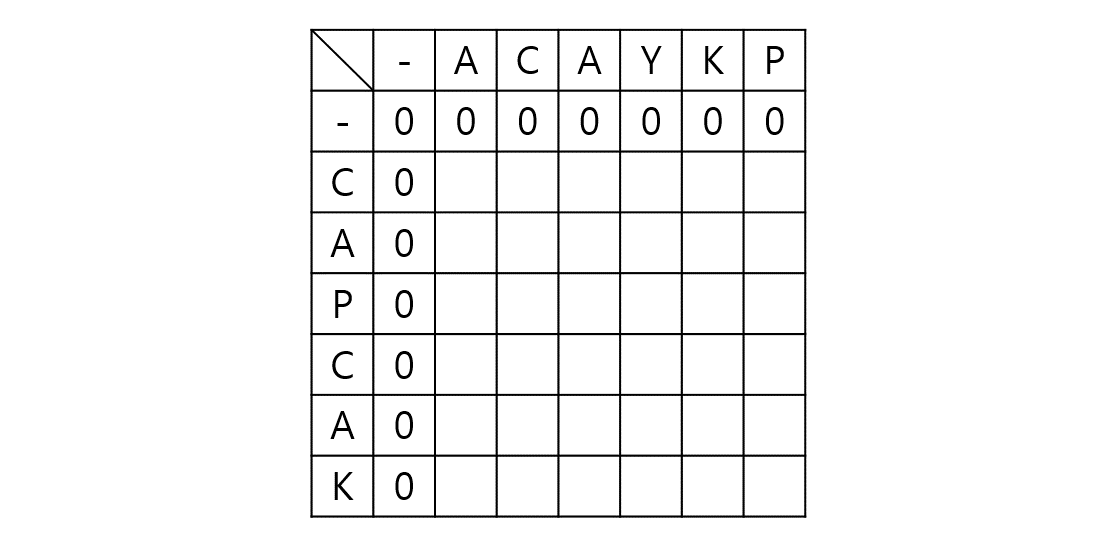
i나 j가 0이면 의미없는 탐색이므로 스킵하고 각각에 대해 1부터 탐색을 진행한다. (글자 조회는 0좌표 기준이므로 1을 뺀다.)
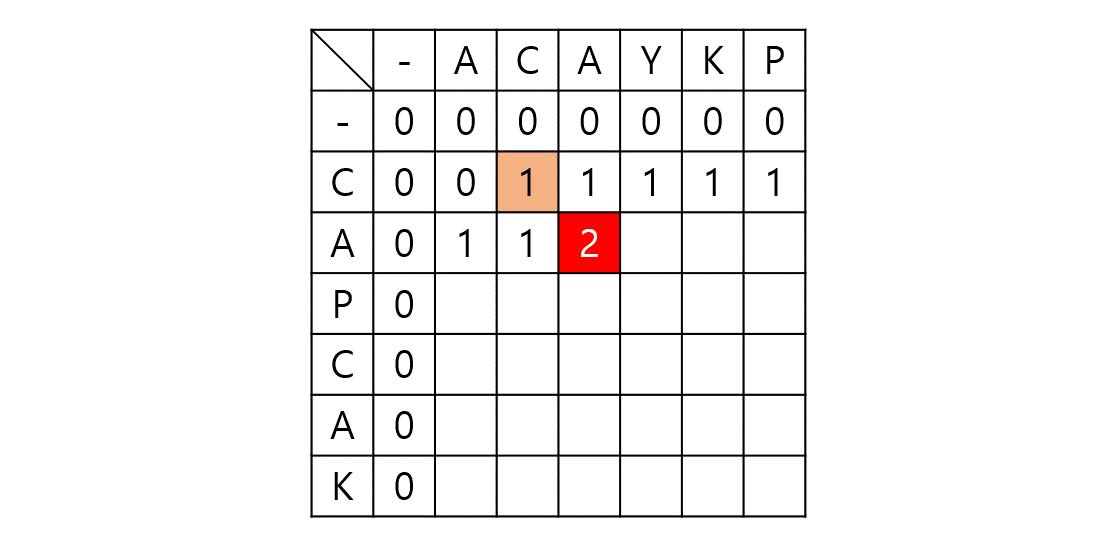
i에 대해 j를 탐색하는 중 i와 j의 글자가 서로 동일 글자일 수 있다. 따라서 Common Character에 매칭이 되는데 둘 다 1칸씩 후퇴하면 sol[i - 1][j - 1]이 있다. 이 값에서 양 쪽이 1칸씩 전진하여 sol[i][j]가 되고 동일 글자가 매칭되었으므로 sol[i][j] = sol[i - 1][j - 1] + 1이 된다.
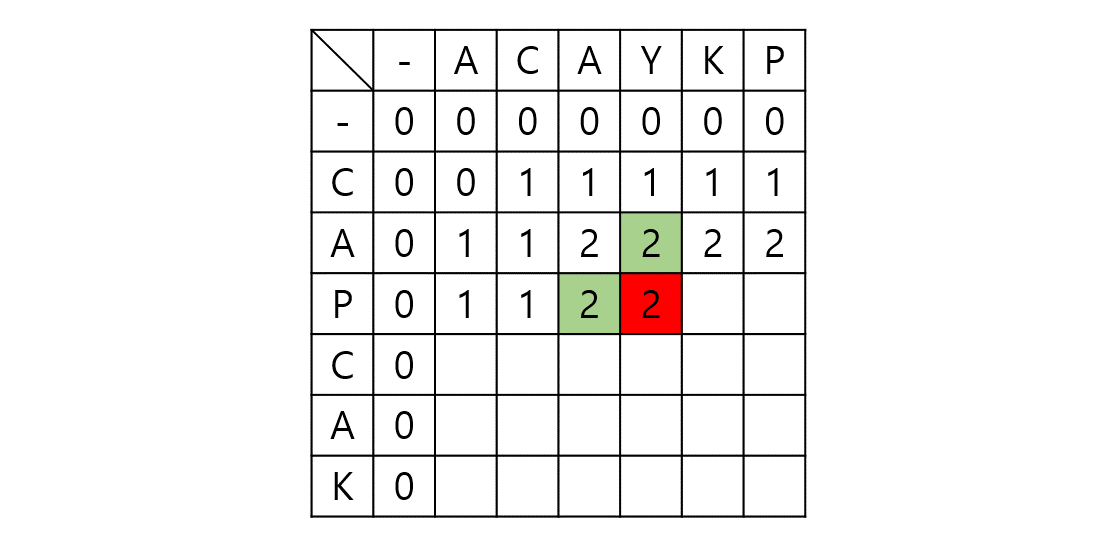
그렇다면 탐색 글자가 서로 동일 글자가 아닌 경우를 보자. 동일 글자가 아닌 경우 j의 C가 없을 경우와 (sol[i][j - 1]) j의 C가 있는데 i의 A가 없을 경우 (sol[i - 1][j])의 값을 서로 비교한 후 그 최대값이 탐색 시점에서의 LCS 값이 되겠다.
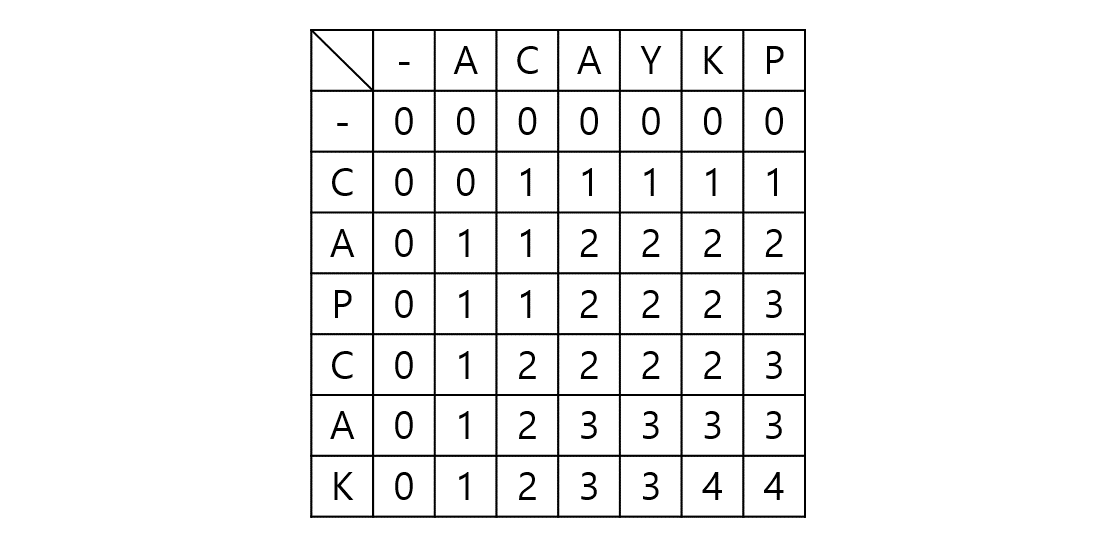
위 그림은 규칙에 따라 탐색을 진행한 결과이다. 탐색을 진행하면서 최댓값을 기록해나가 탐색이 끝나고 최댓값을 출력하면 되겠다.
python 코드
import sys input = sys.stdin.readline A = input().rstrip() B = input().rstrip() sol = 0 dp = [[0 for _ in range(len(A) + 1)] for _ in range(len(B) + 1)] for i in range(1, len(B)): for j in range(1, len(A)): if B[i - 1] == A[j - 1]: # 동일 글자라면 dp[i][j] = dp[i - 1][j - 1] + 1 # 둘다 후퇴한 값에서 + 1 else: dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) sol = max(sol, dp[i][j]) print(sol)
'Algorithms > Baekjoon' 카테고리의 다른 글
| BOJ #11051 이항 계수 2 (0) | 2021.08.10 |
|---|---|
| BOJ #10217 KCM Travel (0) | 2021.08.01 |
| BOJ #11054 가장 긴 바이토닉 부분 수열 (0) | 2021.07.28 |
| BOJ #11444 피보나치 수 6 (0) | 2021.07.28 |
| BOJ #12865 평범한 배낭 (0) | 2021.07.28 |