읽기 전
- 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
- 개인적으로 사용해보면서 배운 점을 정리한 글입니다.
세그먼트 트리?
간격 혹은 세그먼트에 대한 정보를 저장하는 트리이다. 지정된 구간을 쿼리하는 자료구조이다. 일반적으로 구간 합을 구하는데 사용하며 각 구간에 대해 어떤 연산을 할 지에 따라 세그먼트의 내용이 바뀐다. 여기서는 구간합을 저장하는 세그먼트 트리에 대해 다룬다.
일반적인 구간합
길이 N인 배열이 있고 특정 구간 l, r에 대해 원소의 합이든 곱이든 쿼리한다고 하자. 하나씩 순회하면서 연산한 결과를 리턴하면 된다. 만약 길이가 N이면 $O(N)$이다. 그리고 M번 쿼리를 수행한다치면 $O(NM)$이 된다. 뭔가 너무 시간복잡도가 높다. 이 점을 해결하기 위해 도입된 구조가 세그먼트 트리이다.
세그먼트 트리의 크기
구간의 합을 저장해야 하므로 트리를 선언해야 한다. 트리는 루트 노드의 좌표가 1이고 양쪽 자식 노드의 좌표는 각각 2 * idx, 2 * idx + 1이다.
길이가 n = 4인 배열의 구한합을 구한다고 할 때, 만들어진 세그먼트 트리는 높이 3의 포화 이진 트리가 생성되며 노드의 개수는 7이다. 그 결과 아래 그림과 같은 트리가 생성된다.

리프노드는 구간합을 구할 기존 배열의 원소를 의미한다. 리프 노드의 개수가 2의 제곱수라면 $log_{2}(2^k)=e$는 루트노드에서 리프노드까지의 간선 개수를 의미한다. $2^k$는 기존 배열의 길이보다 같거나 작은 2의 제곱수를 의미한다. 즉, 트리의 높이는 $log_{2}(2^k) + 1$이다. 여기서 높이 3인 트리가 갖는 최대 노드 수는 $2^3 - 1= 7$이 되어 생성할 때 길이 7인 배열을 생성해서 구성하면 되겠다. 그렇다면 n이 2의 제곱수가 아니라고 해보자.
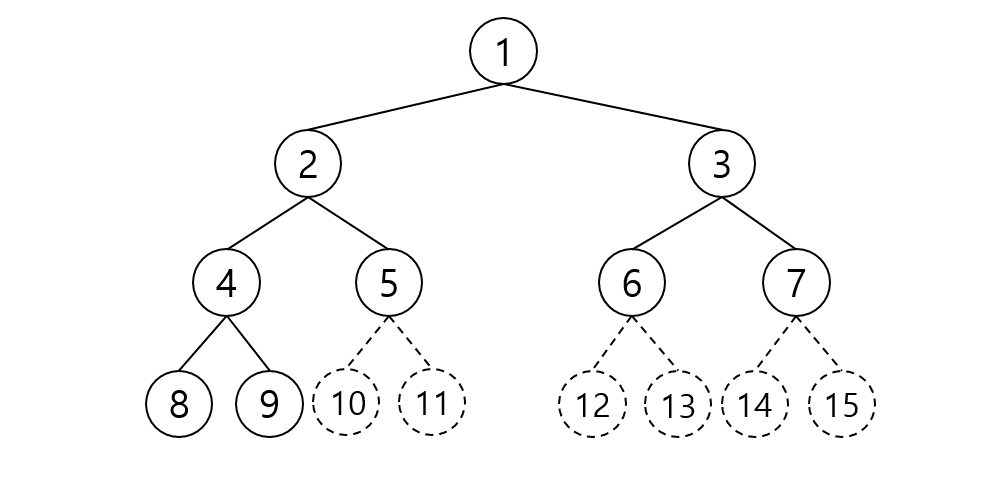
노드 번호 8, 9, 5, 6, 7은 기존 배열의 원소가 되고 나머지는 구간합을 나타낼 것이다. 트리의 높이는 n보다 작은 2의 제곱수 기준으로 루트노드부터 리프노드까지의 간선은 $log_2{2^2} + 1$개이고 거기에 1을 더해 4가 된다. 이를 공식으로 나타내면 $\lceil log_2 n + 1\rceil$이 된다. 높이를 알 수 있으므로 세그먼트 트리 배열은 그 높이가 가질 수 있는 이진 트리 노드의 최댓값을 갖는 배열로 미리 정의해야 한다. 따라서 $2^h - 1$ 길이 배열이 된다. 그림에서 10 ~ 15 번호까지는 할당이 되지 않는데 이 값은 기존 배열이 2의 제곱수가 아니기 때문에 버리는 노드이다.
위와 같이 구성되기 때문에 세그먼트 트리에서 구간합을 쿼리할 때 트리의 높이에 의존하여 시간복잡도가 $log\ n$가 된다. 만약 세그먼트 트리의 높이를 구하기가 귀찮으면 그냥 4n 크기의 배열을 생성하면 된다.
세그먼트 트리 생성
구간합을 쿼리하기 전에 트리에 각 구간의 합을 저장해야 한다. nums = [1, 3, 5, 2, 6, 4]배열에 대해 저장한다고 하자. 세그먼트 트리 생성과정의 기본은 분할 정복이다. 구간을 반으로 쪼개며 진행하되 시작과 끝점이 동일하면 그 원소 자체를 의미하므로 노드에 값을 저장하고 리턴한다. 그리고 윗 단계에서 절반씩 나눠 재귀호출한 결과가 값으로 리턴되었기 때문에 더한 뒤 저장하여 값을 리턴한다. 이 과정을 반복하여 맨 처음 루트 노드에 다다르면 전체 배열 원소의 합이 루트 노드의 값이 된다. 배열을 기준으로 나눠진 값을 보자.

재귀 호출을 하되 저장하는 노드는 좌우측으로 나눈다.
- 좌측 노드의 좌표 : node * 2, 구간 : left - mid
- 우측 노드의 좌표 : node * 2 + 1, 구간 : mid + 1, right
- 현재 노드의 좌표 : node, 구간 : left - right, 값 : 좌/우측 노드의 합
python 코드로 구현해보자.
Python 코드
from math import ceil, log
def init(arr, tree, i, left, right):
if l == r:
tree[i] = arr[l]
return tree[i]
mid = left + (right - left) // 2
tree[i] = init(arr, tree, i * 2, left, mid) + init(arr, tree, i * 2 + 1, mid + 1, right)
return tree[i]
nums = [1, 3, 5, 2, 6, 4]
segment_tree[0] * (pow(2, ceil(log(len(nums), 2) + 1)) - 1)
init(nums, segment_tree, 1, 0, len(nums) - 1)
print(segment_tree)
그림을 보면 알 수 있다시피 1좌표 기준으로 루트 노드에 전체 합이 들어가고 각 자식 노드에 대해 idx * 2, idx * 2 + 1 좌표에 값이 들어감을 알 수 있다. 그리고 쓰이지 않는 자리는 구간이 맞지 않아 할당되지 않았음을 확인할 수 있다.
세그먼트 트리 쿼리
세그먼트 트리 구성을 끝냈으니 이제 각 구간에 대해 쿼리를 하여 구간합을 합리적인 시간에 리턴해야 한다. 원하는 구간 정보가 주어졌을 때 노드의 구간에 대해 네 가지 상황에 대응해야 한다.
구간이 노드의 구간에 완전히 벗어난 경우
의미없는 탐색이므로 그대로 0을 리턴한다.
요청 구간이 노드의 구간을 완전히 포함한 경우
노드의 구간도 구하고자 하는 범위 내에 있으므로 트리 좌표의 값을 리턴한다.
노드의 구간이 요청 구간을 완전히 포함한 경우
아직 더 깊이 탐색해서 요청 구간 외의 잉여 구간을 배제해야 하므로 절반씩 나눠 재귀 탐색을 진행한다.
요청 구간이 노드의 구간에 걸쳐진 경우
3번 상황과 같이 더 깊이 탐색해서 요청 구간 외 잉여 구간을 배제해야 한다.
정리한 결과 분기문은 1, 2번에 대해서만 작성하면 되겠다.
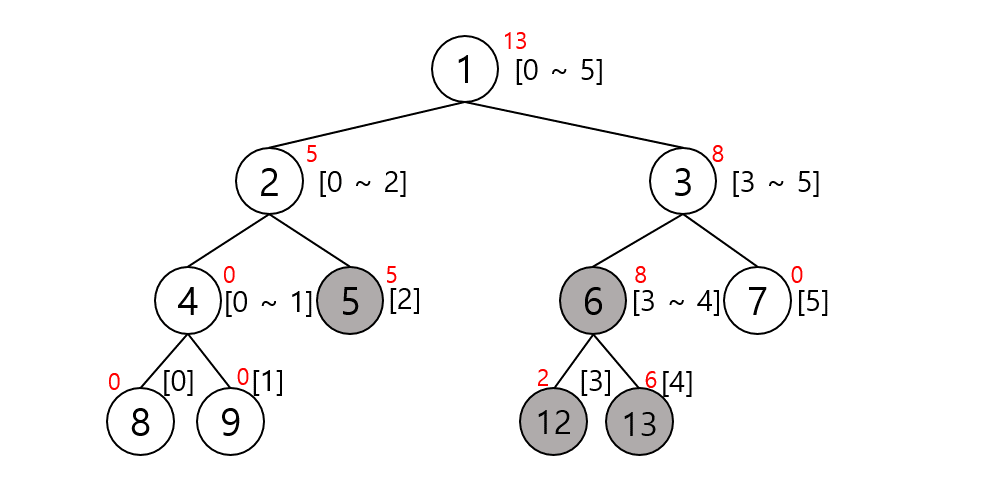
좌표 2부터 4까지의 구간합을 구한다고 해보자. 그렇다면 노드 5와 노드 6의 값만 더하면 된다. 나머지는 구간 밖에므로 4, 7번 노드 탐색 시 0을 리턴한다. 그러면 2, 3 노드에서는 5, 6의 값만 리턴받게 되고 재귀를 처음에 호출한 루트 노드에서 좌표 2, 3, 4 값의 합을 구성해 리턴한다. python 코드로 작성해보자.
python 코드
def search(tree, i, start, end, left, right):
if end < left or right < start:
return 0
if left <= start and end <= right:
return tree[i]
mid = left + (right - left) // 2
return search(tree, i * 2, start, mid, left, right) + search(tree, i * 2 + 1, mid + 1, end, left, right)
print(f'idx 0 to 3 : {nums[0:4]}')
print(f'sum 0 to 3 : {search(tree, 1, 0, len(nums) - 1, 0, 3)}')
세그먼트 트리 갱신
세그먼트 트리를 구성하고 나서 기존 배열의 i번째 원소를 바꾸고 싶은 상황이 있다고 하자. 배열의 원소 한 개가 바뀌었다고 매번 새로 트리를 만들기는 효율이 떨어진다. 구간의 합에 대해 바꾸고자 하는 원소가 포함된 구간만 변경을 가하면 된다. 기존 배열 nums = [1, 3, 5, 2, 6, 4]에서 nums = [1, 3, 5, 4, 6, 4]로 4번째 원소(3번 좌표)를 2에서 4로 변경했을 경우 우선 바꾸고자 하는 인덱스가 포함되지 않은 경우는 의미없는 탐색이므로 그대로 종료하고 구간에 포함될 경우 기존 값과 바뀔 값의 차이를 넘겨 트리의 값에 반영한다. 만약 리프 노드까지 도달하지 못했다면 좌/우로 분할하여 반영하면 되겠다.
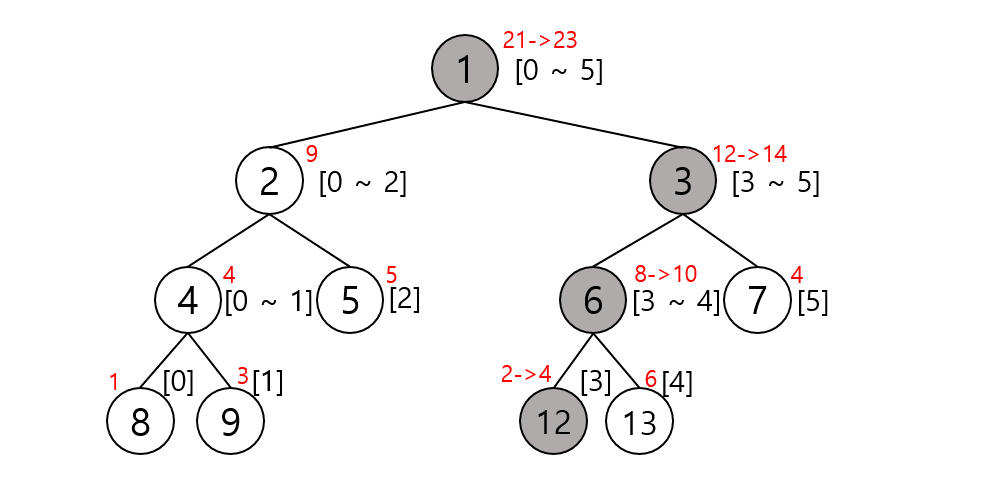
알고리즘에 따르면 회색으로 칠해진 노드의 구간이 바꾸고자 하는 좌표가 포함되어 값이 변경되어야 한다. 이를 python 코드로 구현해보자.
python 코드
def update(tree, i, start, end, idx, diff):
if start > idx or idx > end:
return
tree[i] += diff
if start != end:
mid = left + (right - left) // 2
update(tree, i * 2, start, mid, idx, diff)
update(tree, i * 2 + 1, mid + 1, end, idx, diff)
print(segment_tree)
update(segment_tree, 1, 0, len(nums) - 1, 3, 4 - nums[3])
nums[3] = 4
print(segment_tree)
전체 코드
from math import ceil, log
def init(arr, tree, i, left, right):
if left == right:
tree[i] = arr[left]
return tree[i]
mid = left + (right - left) // 2
tree[i] = init(arr, tree, i * 2, left, mid) + \
init(arr, tree, i * 2 + 1, mid + 1, right)
return tree[i]
def search(tree, i, start, end, left, right):
if end < left or right < start:
return 0
if left <= start and end <= right:
return tree[i]
mid = start + (end - start) // 2
return search(tree, i * 2, start, mid, left, right) + search(tree, i * 2 + 1, mid + 1, end, left, right)
def update(tree, i, start, end, idx, diff):
if start > idx or idx > end:
return
tree[i] += diff
if start != end:
mid = start + (end - start) // 2
update(tree, i * 2, start, mid, idx, diff)
update(tree, i * 2 + 1, mid + 1, end, idx, diff)
nums = [1, 3, 5, 2, 6, 4]
segment_tree = [0] * pow(2, ceil(log(len(nums), 2) + 1))
init(nums, segment_tree, 1, 0, len(nums) - 1)
print(f'idx 0 to 3 : {nums[0:4]}')
print(f'sum 0 to 3 : {search(segment_tree, 1, 0, len(nums) - 1, 0, 3)}')
print(segment_tree)
update(segment_tree, 1, 0, len(nums) - 1, 3, 4 - nums[3])
nums[3] = 4
print(segment_tree)'Algorithms > Data Structure' 카테고리의 다른 글
| 레드-블랙 트리(Red-Black Tree) (2) | 2021.08.26 |
|---|---|
| 세그먼트 트리 비재귀 구현 (0) | 2021.08.16 |
| 최소 신장 트리(Minimum Spanning Tree) (1) | 2021.08.02 |
| 서로소 집합(Disjoint Set), 유니온 파인드(Union-Find) (0) | 2021.08.02 |
| 트라이(Trie) (1) | 2021.07.05 |