스터디룸

읽기 전

• 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
• 개인적으로 배운 점을 정리한 글입니다.

문제 링크

Programmers. 다리를 지나는 트럭

문제 풀이

처음엔 시간복잡도를 생각해 다리 무게와 트럭의 진입, 퇴장 시기를 고려하여 적절히 더하면 되겠다 싶었는데 연산이 너무 이상하게 꼬였다. 다른 풀이를 보니 정말 정직하게 큐를 이용해서 1개씩 count를 하고 있었다. 생각해보니 전체 탐색해봐야 $10^9$으로 대략 1초가 걸려 Python으로 TLE가 걸리지는 않을 것 같았다. 연산이 괜히 복잡해지면 완전 탐색도 고려할 법하다.

이 문제의 핵심은 다리를 0으로 가득 채워진 큐로 선언해서 해결한다는 점이었다.

• 도착한 트럭 개수를 저장할 변수 선언
• 매 탐색마다 다리에서 popleft된 값이 0보다 크면 트럭이므로 현재 적재된 무게에서 빼고 도착한 트럭 대수를 1 더한다.
• 만약 아직 적재할 트럭이 남아있고 맨 앞 트럭 + 현재 적재된 무게가 다리의 용량 이하라면 트럭이 진입해도 되므로 다리에 넣는다.
• 그렇지 않은 경우 기존 적재된 트럭만 전진해야 하므로 0을 넣는다.
• 시간 카운트 + 1

python 코드

from collections import deque
def solution(bridge_length, weight, truck_weights):
    N = len(truck_weights)
    b_weight, arrived = 0, 0
    q = deque([0] * N)
    answer = 0
    while arrived < N:
        exit = q.popleft()
        if truck_weights and truck_weights[0] + b_weight <= weight:
            truck = truck_weights.pop(0)
            b_weight += truck
            q.append(truck)
        else:
            q.append(0)
        answer += 1
    return answer

읽기 전

• 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
• 개인적으로 배운 점을 정리한 글입니다.

문제 링크

Programmers. 도둑질

문제 풀이

직선에서의 똑같은 문제는 막힘없이 풀었는데 원형이 되자마자 막혀버렸다. 첫 집을 방문하면 이전 집(마지막 집)은 방문하면 안된다는 사실을 알아야 한다. 즉, 마지막 값을 방문하려면 첫 집을 방문하지 않아야 함을 의미하므로 dp 배열을 두 개 생성해야 한다.

• 주어진 집의 개수만큼의 dp 배열 생성
• 첫 집은 무조건 방문하는 경우 0, 1번 index 값 설정, 첫 집을 방문하지 않는 경우 0, 1번 index 설정
• 이후 2부터 N - 1까지 i번째 항은 i - 2까지의 최대값과 i번째 집을 더한 값, i - 1까지의 최대값을 비교하여 더 큰값으로 설정한다.
• dp 배열의 최대값들을 비교해 다른 값 리턴

python 코드

def solution(money):
    N = len(money)
    dp1 = [0] * N
    dp2 = [0] * N
    dp1[0], dp1[1] = money[0], max(money[0], money[1])
    dp2[0], dp2[1] = 0, money[1]
    for i in range(2, N):
        if i == N - 1:
            dp1[i] = max(dp1[i - 2], dp1[i - 1])
            dp2[i] = max(dp2[i - 2] + money[i], dp2[i - 2])
            continue
        dp1[i] = max(dp1[i - 2] + money[i], dp1[i - 1])
        dp2[i] = max(dp2[i - 2] + money[i], dp2[i - 1])
    return max(max(dp1), max(dp2))

읽기 전

• 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
• 개인적으로 배운 점을 정리한 글입니다.

문제 링크

Programmers. 등굣길

문제 풀이

바로 풀릴 줄 알았는데 웅덩이가 각 경계선에 있는 경우 그 뒤로는 도달할 수 없음을 간과했다. 만약 시작점 바로 우측과 하단에 웅덩이가 있으면 최단 거리의 개수가 0이 될 수도 있음을 고려하자.

• 최단 거리를 기록할 2차원 배열을 생성한다.
• puddle의 원소마다 해당 자리에 INF를 넣어 갈 수 없음을 표기한다.
• 시작점으로부터 우측, 하단 경계선에 INF가 나오기 전까지 1로 바꾼다.
• [1][1]부터 시작하여 끝점까지 위와 좌측의 값을 더한다. 만약 위/좌측의 값이 INF이면 갈 수 없음을 의미하므로 0으로 간주한다.
• 도착점인 우측 하단의 값을 리턴한다.

python 코드

def solution(m, n, puddles):
    board = [[0] * m for _ in range(n)]
    INF = float('inf')
    for c, r in puddles:
        board[r - 1][c - 1] = INF
    for i in range(1, n):
        if board[i][0] == INF:
            break
        board[i][0] = 1
    for j in range(1, m):
        if board[0][j] == INF:
            break
        board[0][j] = 1
    for i in range(1, n):
        for j in range(1, m):
            if board[i][j] == INF:
                continue
            a = board[i - 1][j]
            b = board[i][j - 1]
            if a == INF:
                a = 0
            if b == INF:
                b = 0
            board[i][j] = (a + b) % 1000000007
    return board[-1][-1]

읽기 전

• 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
• 개인적으로 배운 점을 정리한 글입니다.

문제 링크

Programmers. 소수 찾기

문제 풀이

풀이에 앞서 사전 작업이 조금 필요하다.

• numbers의 종이를 뽑아 숫자를 만드는 함수(Permutation)
• 만든 숫자가 소수인지 확인할 에라토스테네스의 체

위 2가지만 구현할 수 있으면 수월히 풀리는 문제였다. 에라토스테네스의 체의 범위는 numbers로 만들 수 있는 최대의 수 + 1로 잡으면 된다. 숫자는 1개부터 numbers의 길이만큼까지 뽑아서 만들 수 있는 수다.

python 코드

def solution(numbers):
    L = len(numbers)
    def permutation(r):
        buf = []
        visited = [0 for _ in range(L)]
        def gen(buf, sol):
            if len(buf) == r:
                s = int("".join(buf))
                if sieve[s] is True:
                    sieve[s] = None
                    sol += 1
                    return sol
            for i in range(L):
                if not visited[i]:
                    buf.append(numbers[i])
                    visited[i] = 1
                    sol = gen(buf, sol)
                    buf.pop()
                    visited[i] = 0
            return sol
        sol = gen(buf, 0)
        return sol
    N = int("".join(sorted(numbers, reverse=True)))
    sieve = [True] * (N + 1)
    sieve[0], sieve[1] = False, False
    for i in range(2, int(N ** 0.5) + 1):
        if sieve[i] is True:
            for j in range(2 * i, N + 1, i):
                sieve[j] = False
    answer = 0
    for i in range(L + 1):
        answer += permutation(i)
    return answer

읽기 전

• 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
• 개인적으로 사용해보면서 배운 점을 정리한 글입니다.

크루스칼 알고리즘이란?

최소 신장 트리(Minimum Spanning Tree) 구현에 사용되는 알고리즘으로 가중치 그래프의 모든 간선들을 대상으로 "1) 최소 비용의 간선으로 구성, 2) 사이클을 형성하지 않음"의 조건을 지켜가며 각 단계마다 사이클을 이루지 않는 최소 비용 간선을 선택하여 최소 신장 트리를 완성하는 알고리즘이다. 프림 알고리즘과 마찬가지로 매 단계마다 최선의 해를 선택하기에 그리디 알고리즘에 바탕을 둔다.

크루스칼 알고리즘의 동작

1. 그래프의 간선들을 가중치 기준으로 오름차순 정렬한다.
2. 정렬된 간선들 중 순서대로 사이클을 형성하지 않는 간선들을 채택한다.
3. 선택된 간선을 MST 집합에 넣는다.
4. MST 집합의 원소 개수가 V - 1개가 될 때까지 2, 3을 반복한다.

사이클 생성 여부를 체크하는 알고리즘은 서로소 집합(Disjoint Set), 유니온 파인드(Union-Find)에 정리하였다.

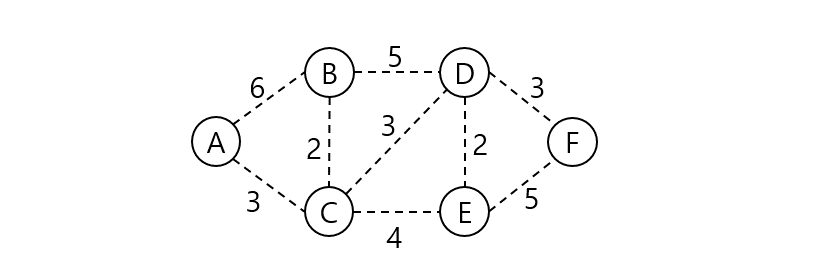
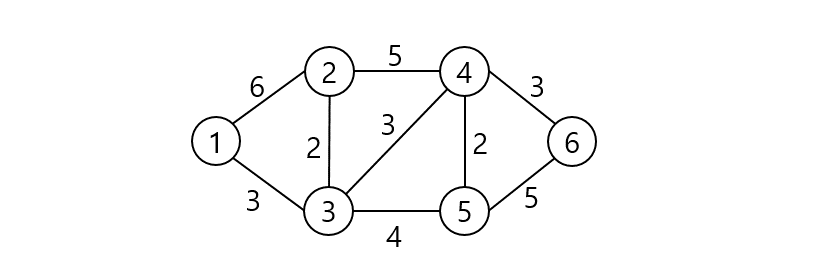
위 그래프의 최소 신장 트리를 크루스칼 알고리즘으로 구해보자.

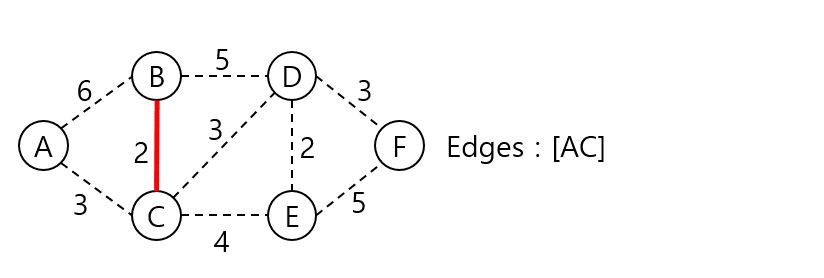
중복된 가중치가 있으나 연결 정점이 작은 순으로 시작하여 BC 간선에서 시작될 것이다.

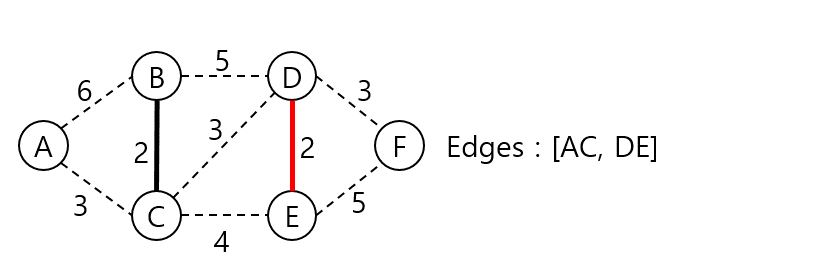
BC 간선 이후 DE 간선의 가중치가 가장 작으니 DE 간선을 MST 집합에 넣는다.

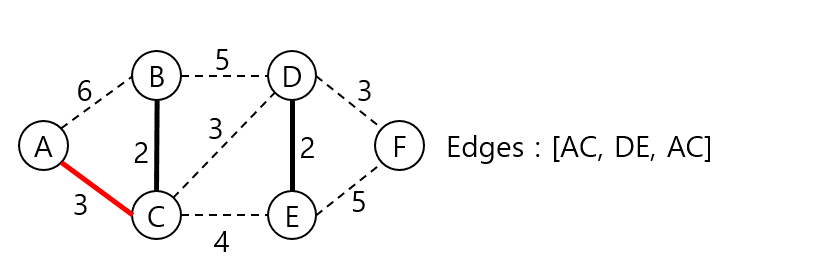
AC, CD, DF 간선의 가중치가 모두 동일하다. 순서대로 사이클을 형성하는지 체크한 결과 모두 사이클을 이루지는 않으니 AC 간선을 MST 집합에 넣는다.

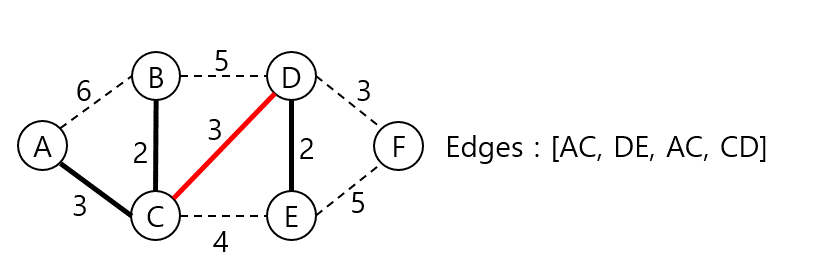
CD, DF의 간선의 가중치가 동일하다. 앞에서 사이클 여부를 체크한 결과 모두 형성하지 않았으므로 CD 간선을 MST 집합에 넣는다.

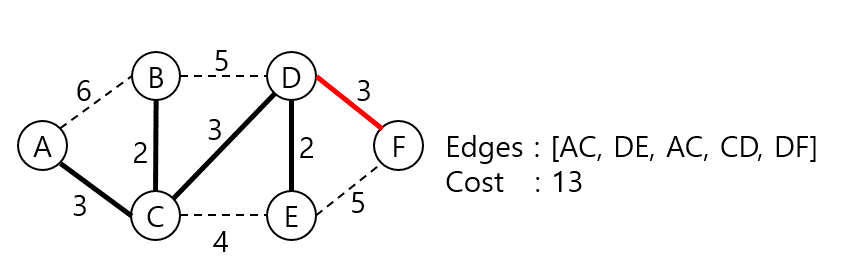
그 다음 가중칙 가장 작은 간선은 DF다. DF도 사이클을 형성하지 않으니 MST 집합에 넣어준다. MST 집합에 포함된 간선의 개수가 V - 1개가 되었으므로 탐색을 중단한다. 최소 신장 트리의 비용은 MST 집합에 속한 간선들의 가중치 합으로 13이 되겠다.

크루스칼 알고리즘의 구현

동작 과정을 보면 사이클을 찾는 과정에서 기존 서로소 집합(Disjoint Set), 유니온 파인드(Union-Find)는 클래스로 정의했지만 여기서는 함수로 구현해야겠다.

Python 코드

from collections import deque


def mst():
    def upward(buf, idx):
        parent = mst_nodes[idx]
        if parent < 0:
            return idx
        buf.append(idx)
        return upward(buf, parent)

    def find(idx):
        buf = []
        result = upward(buf, idx)
        for i in buf:
            mst_nodes[i] = result
        return result

    def union(x, y):
        x, y = find(x), find(y)
        if x == y:
            return False
        if mst_nodes[x] < mst_nodes[y]:
            mst_nodes[y] = x
        elif mst_nodes[x] > mst_nodes[y]:
            mst_nodes[x] = y
        else:
            mst_nodes[x] -= 1
            mst_nodes[y] = x
        return True

    V, E = 6, 9
    edges = [[1, 2, 6], [1, 3, 3], [2, 3, 2], [2, 4, 5],
             [3, 4, 3], [3, 5, 4], [4, 5, 2], [4, 6, 3], [5, 6, 5]]
    edges.sort(key=lambda x: x[2])
    mst_graph = [[0] * V for _ in range(V)]
    mst_nodes = [-1 for _ in range(V)]
    mst = []
    cost = 0
    q = deque(edges)
    while True:
        u, v, w = q.popleft()
        udx, vdx = u - 1, v - 1
        if union(udx, vdx) is False:
            continue
        mst.append((u, v))
        mst_graph[udx][vdx] = 1
        mst_graph[vdx][udx] = 1
        cost += w
        if len(mst) == V - 1:
            break
    print(f'mst cost is {cost}')
    print(mst)
    for row in mst_graph:
        print(*row)


mst()

크루스칼 알고리즘의 시간복잡도

union-find 알고리즘은 시간복잡도가 상수이므로 간선들을 가중치 기준으로 정렬하는 데 걸리는 시간에 의존한다. 일반적인 경우 빠른 정렬 알고리즘의 시간복잡도는 $O(nlog\ n)$이므로 이 경우 $O(Elog\ E)$가 된다. 우선순위 큐를 사용한 프림 알고리즘의 시간복잡도인 $O(Elog\ V + Vlog\ V)$​과 비교했을 때 간선의 수가 적은 Sparse Graph의 경우 크루스칼 알고리즘이 유리하고 간선의 수가 많은 Dense Graph의 경우 프림 알고리즘이 유리하다.

• Sparse Graph는 크루스칼 알고리즘이 유리
• Dense Graph는 프림 알고리즘이 유리

관련 링크

최소 신장 트리(Minimum Spanning Tree)

프림 알고리즘(Prim's Algorithm

서로소 집합(Disjoint Set), 유니온 파인드(Union-Find)