스터디룸

읽기 전

• 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
• 개인적으로 사용해보면서 배운 점을 정리한 글입니다.

플로이드-워셜 알고리즘이란?

플로이드 워셜 알고리즘은 그래프에서 가능한 모든 정점에 대해 최단거리를 구하는 알고리즘이다. 다익스트라 알고리즘은 V번 수행도 가능은 하나 코드 구현 측면에서 조금 더 복잡하며 일반적으로 다익스트라 알고리즘의 시간복잡도는 $O(Elog\ V)$로 표현되는데 V번 수행하므로 $O(VElog\ V)$가 되어 플로이드 워셜보다 불리해진다.

플로이드-워셜 알고리즘의 동작

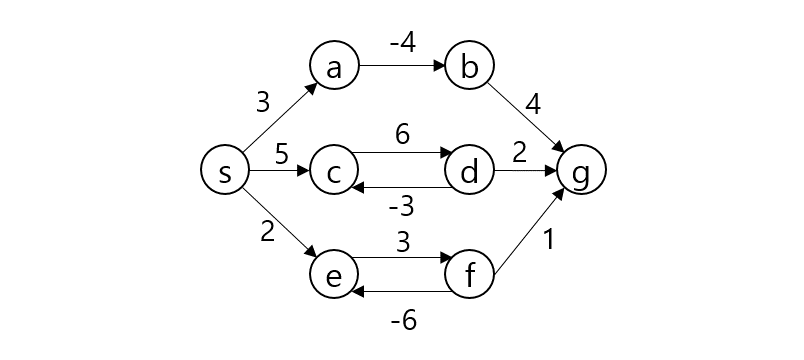
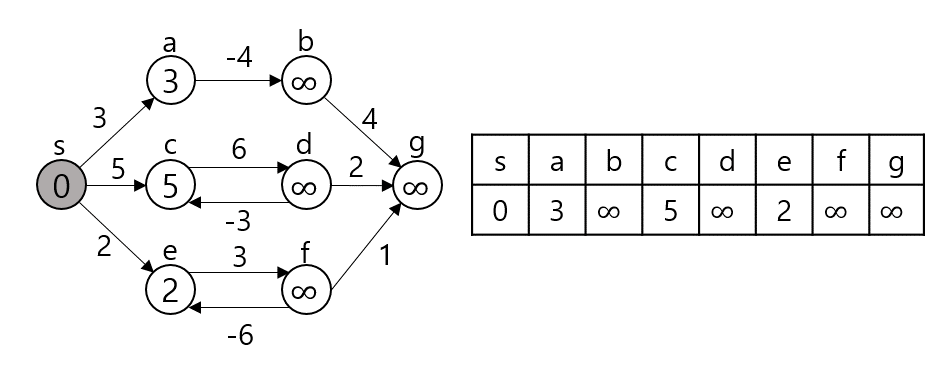
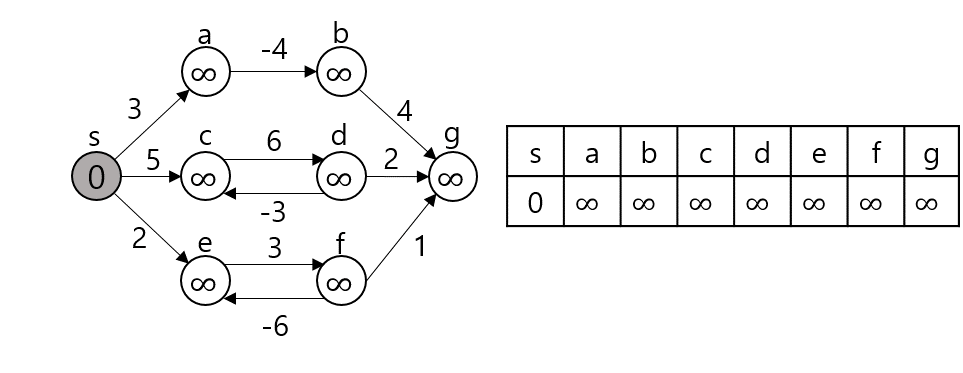
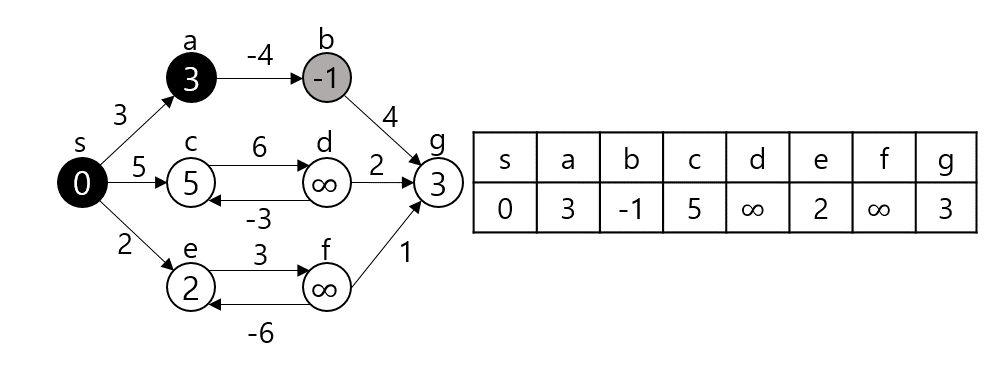
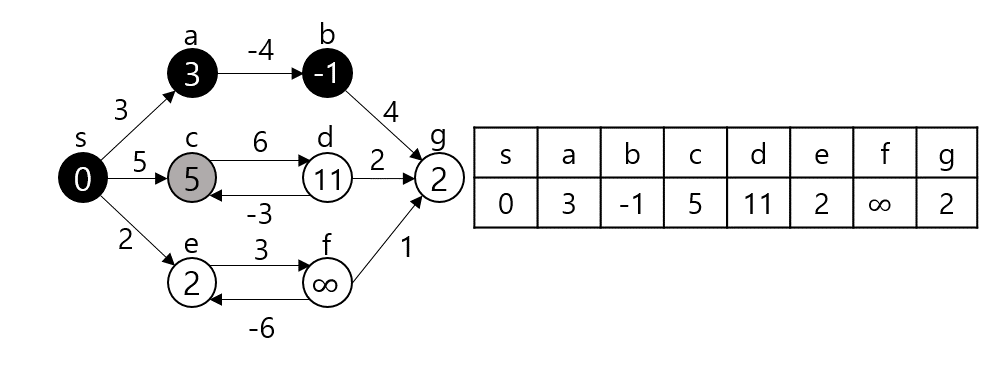
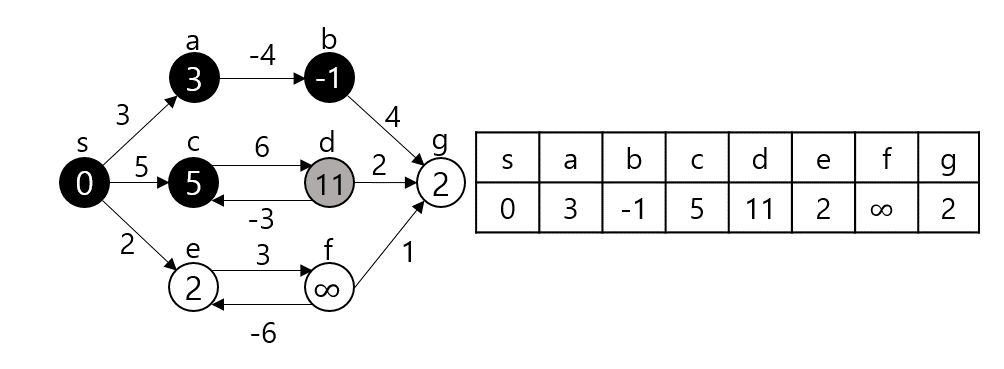
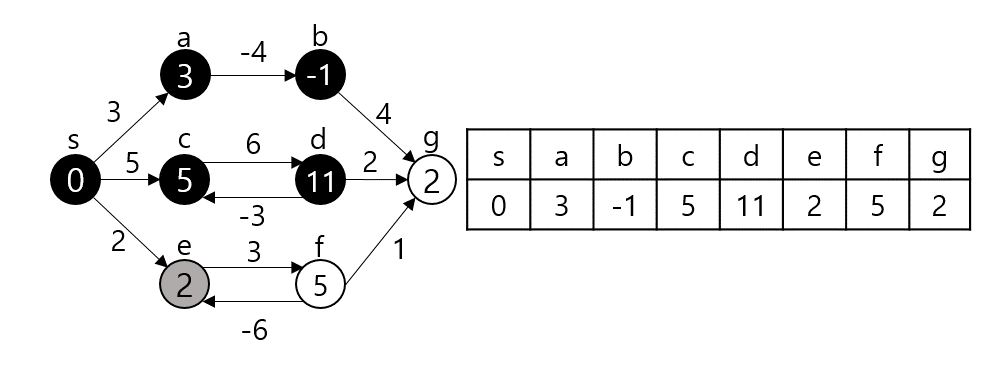
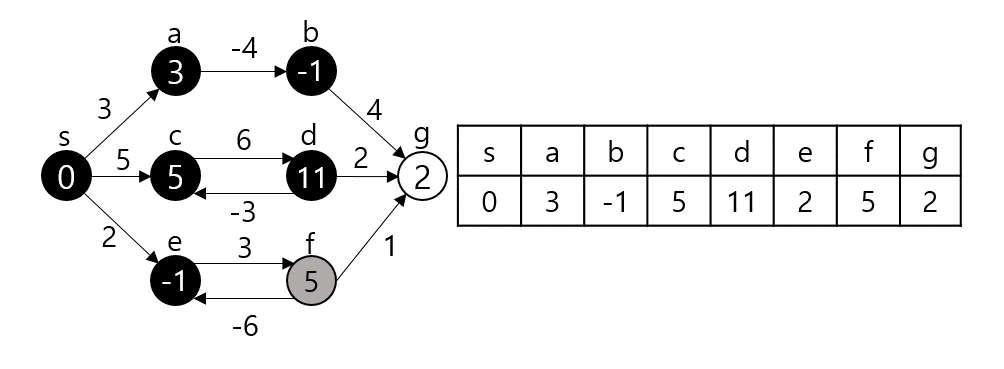
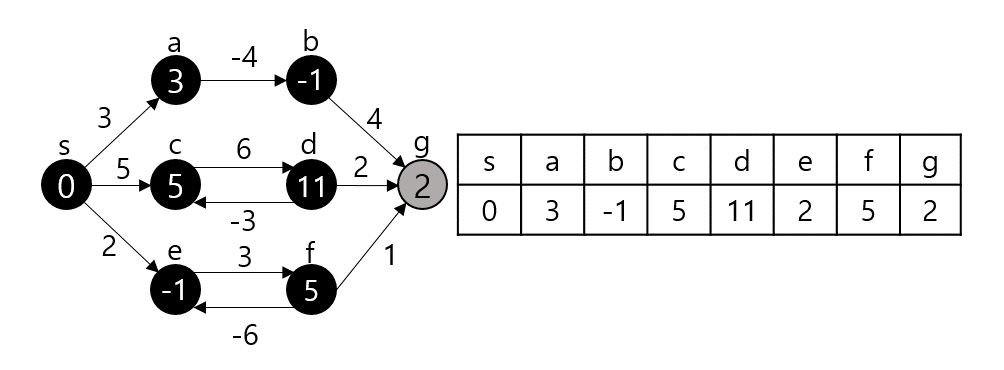
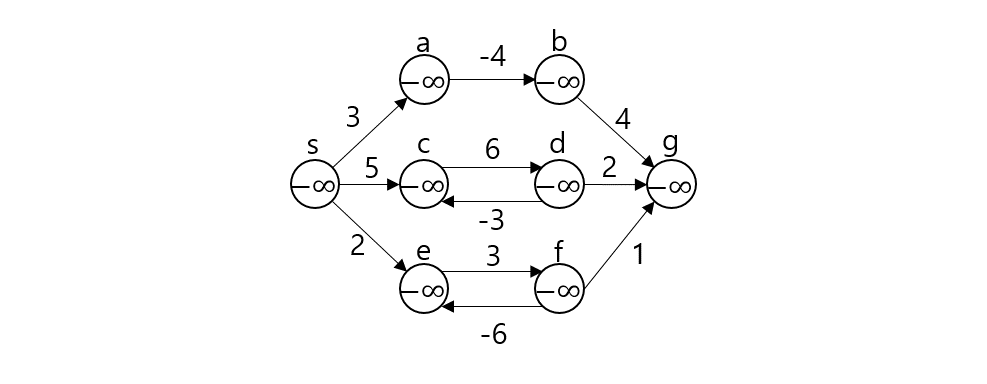
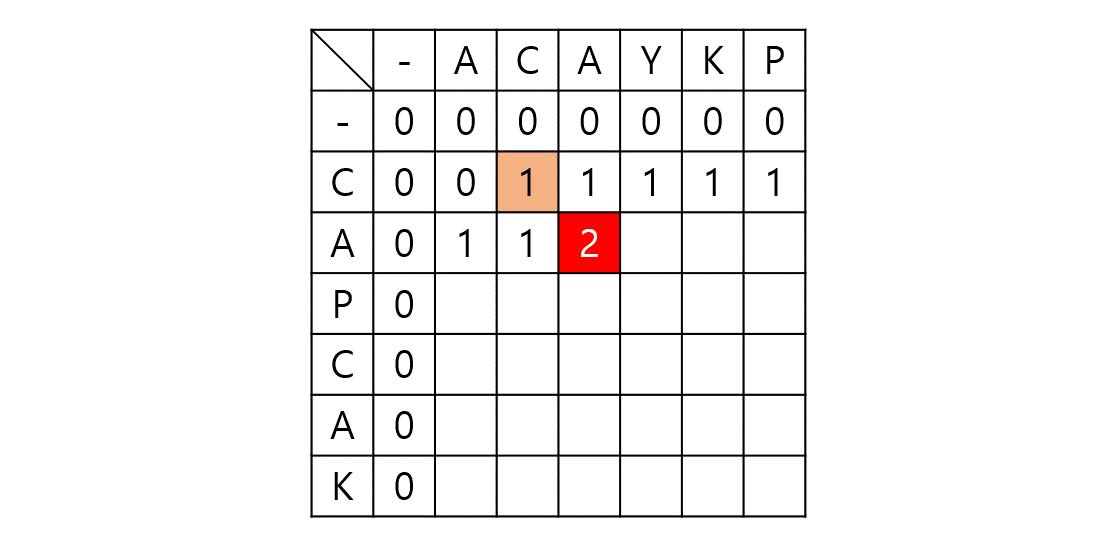
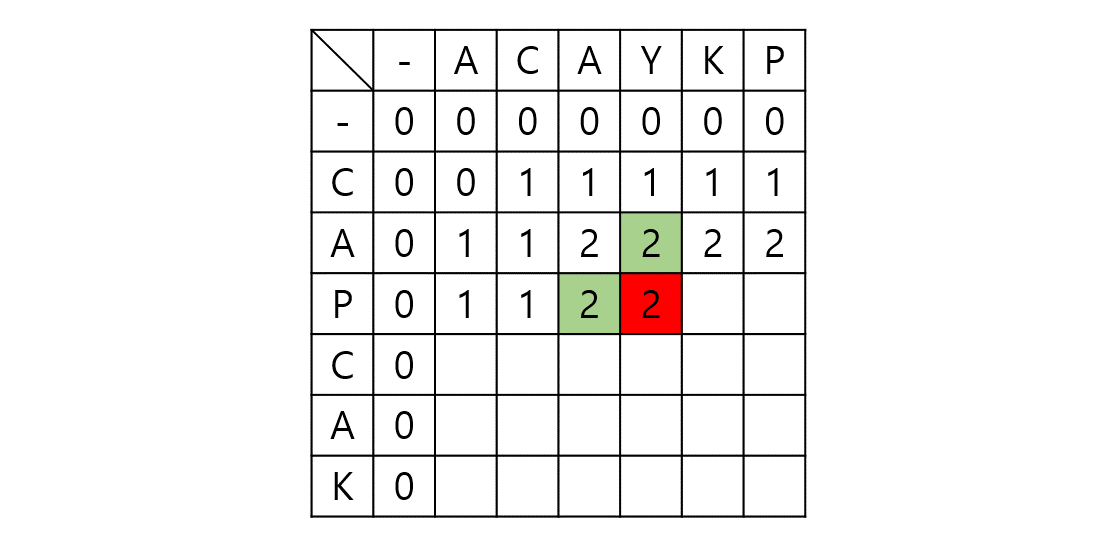
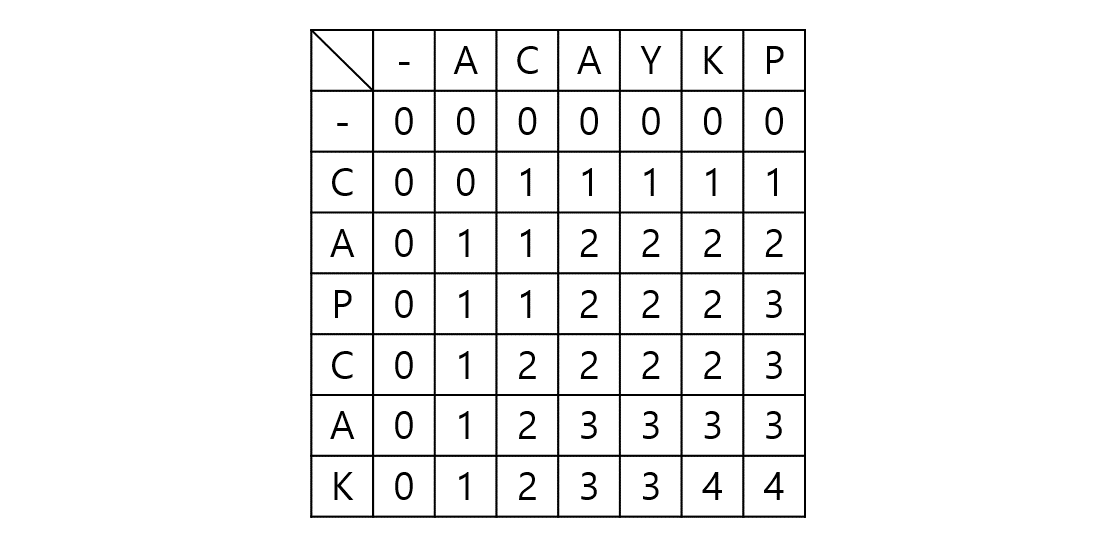
임의의 노드 s에서 임의의 노드 t까지 간다고 가정하자. 그렇다면 s와 t 사이의 노드 m에 대해 s - m까지의 최단거리와 m - t까지의 최단거리를 이용한다. (Optimal Substructure(Dynamic Programming), Edge Relaxation 과정이라고도 부른다.) dist[s][t]를 s에서 t로 가는 최단 거리라 하자. 만약 s, t가 서로 연결되어 있다면 그 간선의 가중치로, 그렇지 않다면 INF로 초기화될 것이다.

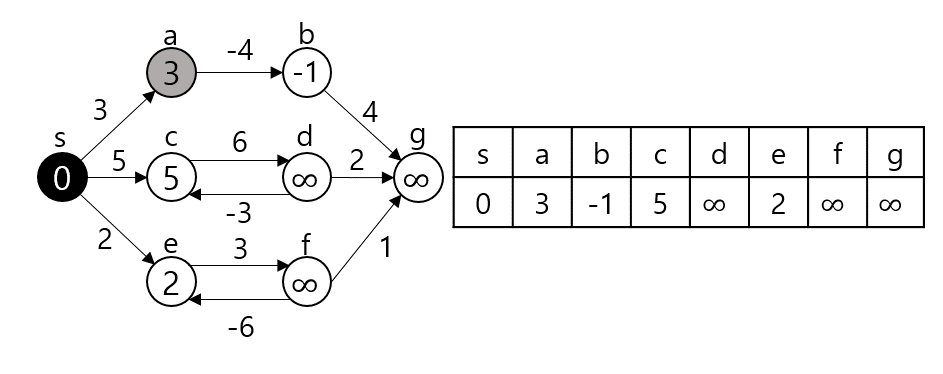
dist[s][t]를 구하는 과정은 s, t 사이의 모든 노드 m에 대해 dist[s][t]와 dist[s][m] + dist[m][t]값을 비교하여 갱신한다.

만약 $s - p_1-p_2-t$가 최단 경로라 할 때 $p_1$ 탐색 시점에서 dist[s][e]가 갱신되고 $p_2$ 탐색시점에서 또 갱신된다. 이런 식으로 모든 V에 대해 탐색을 진행하므로 시간복잡도는 $O(|V^3|)$이 된다.

음수 간선의 영향 및 음수 사이클 검출

벨만-포드 알고리즘(Bellman-Ford Algorithm)과 마찬가지로 그래프의 간선에 음수가 존재할 경우 그래프의 음수 사이클이 발생하지 않는다면 최단 거리가 성립함을 의미하므로 정상적으로 탐색이 가능하다. 벨만-포드 알고리즘은 $|V| - 1$번째 탐색 후 V번째 탐색 시 갱신되는 값이 있으면 음수 사이클이 있다고 결론을 내렸었다. 플로이드 워셜 알고리즘은 조금 다르다.

플로이드 워셜 알고리즘에서의 음수 사이클 검출은 자기 자신에게 가는 간선 거리를 검사하면 된다. 당연히 자기 자신을 경로로 갖는 Loop Edge가 존재하고 그게 음수 가중치를 갖지 않는 한 자기 자신의 경로는 항상 0이어야 한다. 그러나 음수 사이클이 존재한다면 음수 사이클에서 적당히 순회한 뒤 다시 자기자신을 재방문하면 음수가 되고 그게 최단 거리로 취급될 것이다.

따라서 임의의 i번째 노드에 대해 dist[i][i] < 0이면 해당 그래프는 음수 사이클을 갖고 있음을 알 수 있다.

python 코드

def floyd-warshall():
    INF = float('inf')
    V, E = map(int, input().split()) # 노드와 간선 개수 입력받는다 가정
    dist = [[INF] * V for _ in range(V)] # 노드는 0부터 V - 1까지
    for i in range(V):
        dist[i][i] = 0
    for _ in range(E):
        s, d, w = map(int, input().split())
        board[s][d] = w
    for m in range(V):
        for s in range(V):
            for t in range(V):
                dist[s][t] = min(dist[s][t], dist[s][m] + dist[m][t])
                # 출발-도착점까지의 거리를 m을 경유했을 때와 비교
    for i in range(V):
        if dist[i][i] < 0:
            # 자기자신의 경로길이가 음수면 음수 사이클 검출
            return -1
    return dist

읽기 전

• 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
• 개인적으로 사용해보면서 배운 점을 정리한 글입니다.

벨만-포드 알고리즘이란?

한 노드에서 다른 노드까지의 최단 거리를 구하는 알고리즘이다. 다익스트라 알고리즘이 모든 가중치가 양수인 경우에만 사용할 수 있는 반면에 벨만-포드 알고리즘은 노드 간의 간선 가중치가 음수인 경우에도 사용할 수 있다. 다만 시간 복잡도는 벨만-포드가 더 크기 때문에 가중치가 모두 양수라면 굳이 벨만-포드를 사용할 필요가 없다.

음수 사이클이 문제가 되는 이유

• 단순 음수 간선일 경우 : 단순 경로이므로 그대로 가중치를 계산하면 된다.
• 사이클이 존재하나 양수값이 더 클 경우 : 사이클을 순환하여도 이득이 없으므로 그대로 진행한다.
• 사이클이 존재하고 음수값이 더 클 경우 : 사이클을 순환할 수록 가중치가 감소해 최소 비용을 찾는 입장에서 사이클을 무한히 순환하고 목적지에 도착함은 실질적인 최단 경로라 보기 어렵다. 적어도 동일 노드를 방문하면 안된다는 등 제약 조건이 있어야 할 것이다.

최단 거리는 순화뇌어서는 안된다는 가정을 담고 있으므로 경로(Edge) 길이는 $|V| - 1$이 된다.

벨만-포드 알고리즘의 동작

1. 시작 노드를 설정한다.
2. 시작 노드에서 각 다른 노드의 거리 값을 무한대로 설정하고 시작 노드를 0으로 설정한다.
3. 현재 노드의 모든 인접 노드를 탐색하며 기존에 저장된 인접 노드까지의 거리보다 현재 노드를 거치고 인접 노드에 도달하는 게 더 짧을 경우 값을 갱신한다.
4. 3의 과정을 모든 노드에 대해 수행한다.
5. 모든 노드에 3 - 4를 수행하고서 또 거리가 갱신된다면 $-\infty$를 발생시키는 음수 사이클이 존재함을 의미한다.

위 그래프는 음수 사이클이 존재하지만 일단 벨만-포드 알고리즘을 적용하여 최단 거리 구하는 과정을 살펴보자. 시작점은 s라 한다.

우선 시작 노드를 0으로 초기화하고 나머지 노드에 대해 $\infty$으로 설정한다.

s의 인접노드는 a, c, e로 각각 3, 5, 2로 저장한다. (INF보다 작기 때문)

s의 인접노드를 모두 탐색했으니 a노드를 현재 노드로 옮긴다. a의 인접노드는 b노드 뿐으로 -1 < INF이므로 -1이 된다.

b 노드의 인접 노드는 g 노드 뿐으로 $-1 + 4 < INF$이기에 3으로 설정한다.

c 노드의 인접 노드는 d 뿐이고 c에서 d로 가는 최단 경로는 $11 < INF$이므로 11이 된다.

d 노드의 인접 노드는 g로 $11 + 8 > 3$으로 그대로 3을 유지한다.

e 노드의 인접 노드는 f이고 $INF > 5$이므로 f에 5를 저장한다.

f의 인접 노드는 e와 g로 e의 경우 $5-6 < 2$로 e를 -1로 갱신하고 g는 $5 + 7 > 3$으로 3을 유지한다. g의 인접 노드는 없으니 첫 번째 탐색을 종료한다. 이후 노드 개수 - 1만큼 반복하면 된다.

이로써 V - 1 개의 노드에 대해 모두 탐색을 종료했다. 그런데 그래프에서 볼 수 있듯이 e와 f 사이엔 음수 사이클이 존재하여 해당 사이클을 무한히 순회하면 모든 노드에 대해 $-\infty$가 될 수 있다. 따라서 위 과정처럼 동일 노드를 방문하지 않는다는 제약조건이 없다면 그대로 -1 등을 출력하여 경로가 존재할 수 없음을 표현해야 한다.

음수 사이클의 존재 여부 검출은 간단하다 V - 1번만큼 탐색을 마쳤으므로 최단 거리 제약 한계에 도달했다. 이 다음 순회에서도 만약 갱신되는 값이 존재한다면 앞으로도 계속 갱신됨을 의미하므로 음수 사이클이 존재함을 의미한다.

벨만-포드 알고리즘의 시간 복잡도

우선 $|V| - 1$번만큼 순회하므로 $O(V)$가 되고 매번 총 edge($O(E)$)만큼 탐색하므로 $O(|V||E|)$가 된다. 그런데 desne graph라면 E는 $V^2$에 근사해지므로 최악의 경우 $O(V^3)$이 된다. 이는 다익스트라 알고리즘이 최악의 경우 $O(V^2)$인 것과 비교했을 때 불리함을 알 수 있다. 따라서 벨만-포드 알고리즘은 간선의 가중치에 음수가 존재할 경우에만 채택해야 한다. 일종의 음수 가중치 지원에 대한 trade off 정도로 생각해야겠다.

python 코드

INF = float('inf')
V, E = map(int, input().split())
edges = []
for _ in range(E):
    s, d, w = map(int, input().split())
    edges.append((s, d, w))
def bellman-ford(start):
    dist = [INF] * (V + 1)
    dist[start] = 0
    for i in range(V):
        for s, d, w in edges:
            if dist[s] != INF and dist[d] > dist[s] + w:
                if i == V - 1:
                    return -1
                dist[d] = dist[s] + w
    return dist    

print(bellman-ford(0))

읽기 전

• 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
• 개인적으로 배운 점을 정리한 글입니다.

문제 링크

BOJ #9251 LCS

문제 풀이

LCS(Longest Common Subsequences) 문제는 두 문자열이 주어졌을 때 모두의 부분 문자열이 되는 문자열 중 가장 긴 문자열을 찾는 문제이다. 경험해보지 않으면 풀기가 상당히 까다로워 정리하고자 한다.

예시에 나와있듯이 ACAYKP와 CAPCAK의 LCS를 찾는다고 해보자. 우선 2차월 배열을 생성하고 0으로 초기화한다.

i나 j가 0이면 의미없는 탐색이므로 스킵하고 각각에 대해 1부터 탐색을 진행한다. (글자 조회는 0좌표 기준이므로 1을 뺀다.)

i에 대해 j를 탐색하는 중 i와 j의 글자가 서로 동일 글자일 수 있다. 따라서 Common Character에 매칭이 되는데 둘 다 1칸씩 후퇴하면 sol[i - 1][j - 1]이 있다. 이 값에서 양 쪽이 1칸씩 전진하여 sol[i][j]가 되고 동일 글자가 매칭되었으므로 sol[i][j] = sol[i - 1][j - 1] + 1이 된다.

그렇다면 탐색 글자가 서로 동일 글자가 아닌 경우를 보자. 동일 글자가 아닌 경우 j의 C가 없을 경우와 (sol[i][j - 1]) j의 C가 있는데 i의 A가 없을 경우 (sol[i - 1][j])의 값을 서로 비교한 후 그 최대값이 탐색 시점에서의 LCS 값이 되겠다.

위 그림은 규칙에 따라 탐색을 진행한 결과이다. 탐색을 진행하면서 최댓값을 기록해나가 탐색이 끝나고 최댓값을 출력하면 되겠다.

python 코드

import sys
input = sys.stdin.readline

A = input().rstrip()
B = input().rstrip()
sol = 0
dp = [[0 for _ in range(len(A) + 1)] for _ in range(len(B) + 1)]
for i in range(1, len(B)):
    for j in range(1, len(A)):
        if B[i - 1] == A[j - 1]: # 동일 글자라면
            dp[i][j] = dp[i - 1][j - 1] + 1 # 둘다 후퇴한 값에서 + 1
        else:
            dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
        sol = max(sol, dp[i][j])
print(sol)

읽기 전

• 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
• 개인적으로 배운 점을 정리한 글입니다.

문제 링크

BOJ #11054 가장 긴 바이토닉 부분 수열

문제 풀이

LIS 응용 문제다. i 번째 좌표에 대해 좌측으로부터의 LIS 길이와 우측까지의 LDS 길이를 산출해서 더한 뒤 자기 자신은 두 번 더했으므로 1을 빼면 된다.

• i좌표에 대한 LIS 배열 생성 (좌측에 대한)
• i좌표에 대한 LDS 배열 생성 (우측에 대한)
• i좌표에 대해 LIS[i] + LDS[i] - 1이 최대가 되는 값 출력

python 코드

import sys
input = sys.stdin.readline

N = int(input())
nums = list(map(int, input().split()))
lis = [0 for _ in range(N)]
lds = [0 for _ in range(N)]
for i in range(N):
    b = 0
    for j in range(i):
        if nums[i] > nums[j]:
            b = max(b, lis[j])
    lis[i] = b + 1
for i in range(N - 1, -1, -1):
    b = 0
    for j in range(N - 1, i, -1):
        if nums[i] > nums[j]:
            b = max(b, lds[j])
    lds[i] = b + 1
sol = 0
for i in range(N):
    sol = max(sol, lis[i] + lds[i] - 1)
print(sol)

읽기 전

• 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
• 개인적으로 배운 점을 정리한 글입니다.

문제 링크

BOJ #11444 피보나치 수 6

문제 풀이

주어진 입력이 너무나도 크다. $O(n)$으로 구해도 답이 없는 수준이다. 따라서 기존 DP 기반으로 피보나치 수를 구하면 여지없이 시간초과가 날 것이다. 따라서 제곱의 형태로 곱해나가 정답을 도출하는 $O(log\ n)$해법을 생각해내야 한다.

이 문제는 초기값을 $\begin{pmatrix}f_2&f_1\f_1&f_0\end{pmatrix}$으로 설정해두고 그에 대한 제곱값이 피보나치 수의 형태로 만들어진다는 사실을 모르면 해결하기가 쉽지 않다. $\begin{pmatrix}f_2&f_1\f_1&f_0\end{pmatrix}= \begin{pmatrix}1&1\1&0\end{pmatrix}$이고 $\begin{pmatrix}1&1\1&0\end{pmatrix}^2=\begin{pmatrix}2&1\1&1\end{pmatrix}=\begin{pmatrix}f_3&f_2\f_2&f_1\end{pmatrix}$임을 알 수 있어 이 점을 이용해야 한다.

python 코드

import sys
input = sys.stdin.readline

def mutiply(arr1, arr2):
    R, C, M = len(arr), len(arr2[0]), len(arr1[0])
    sol = [[0 for _ in range(C)] for _ in range(R)]
    for i in range(R):
        for j in range(C):
            b = 0
            for k in range(M):
                b += arr1[i][k] * arr2[k][j]
            sol[i][j] = b % 1000000007
    return sol

def solve(n):
    if n == 1:
        return matrix
    t = solve(n // 2)
    t = multiply(t, t)
    if n % 2 == 1:
        t = multiply(t, matrix)
    return t
N = int(input())
matrix = [[1, 1], [1, 0]]
if N > 1: # N이 1보다 크면
    result = solve(N - 1) # [0][0]은 f_2부터 시작이므로 N - 1을 입력
    print(result[0][0])
else: # N이 1이면
    print(matrix[0][0])