읽기 전
- 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
- 개인적으로 사용해보면서 배운 점을 정리한 글입니다.
고등수학 교과과정에 포함되어 있으나 순서쌍을 생성하는 코드는 잘 모르고 있어 정리하게 되었다. backtracking 등 완전 탐색에 많이 쓰이는 데 전체 원소에 대한 순열이 아니라 특정 개수만을 뽑는 경우를 정리해보려 한다.
순열 순서쌍 생성하기
순열(Permutation)은 서로 다른 n개의 대상에서 r개를 추출해 나열된 순서쌍을 의미하며 그 경우의 수에 대한 표현은 $ _{n}P_r(0\le r\le n)$이다. n과 r이 같을 때 순열의 경우의 수는 n!이 된다. (n개의 자리에 n개의 원소가 나열될 경우의 수) 공식은 고등학교에서 배웠듯이 $\cfrac{r!}{(n-r)!}(0\le r \le n)$ 이다.
이제 iterable한 객체를 입력받아 추출할 원소의 개수 r을 입력받았을 때 생성할 수 있는 순열의 순서쌍을 출력하자.
python 코드
def permutation(arr, r):
arr = sorted(arr) # 이쁘게 만들기 위해
result = [] # 중간값 저장
visited = [0 for _ in range(len(arr))] # 방문 체크
def generate(buf):
if len(buf) == r: # 만약 모두 추출했으면
result.append(list(buf)) # 주소 재할당 후 저장
return # 종료
for i in range(len(arr)): # 모든 원소에 대해
if not visited[i]: # 아직 사용되지 않은 원소라면
buf.append(arr[i]) # 중간결과에 추가
visited[i] = 1 # 방문체크
generate(buf) # 재귀호출
buf.pop() # backtracking
visited[i] = 0 # backtracking
generate([])
return result
data = "ABC"
for i in range(1, len(data) + 1):
print(["".join(x) for x in permutation(data, i)])
data = [1, 2, 3]
print(permutation(data, 2))

위 코드는 재귀 방식으로 구현되었다. result에 buf를 더하는 시점에 relocate 하지 않아 메모리 주소 재할당이 이루어지지 않으면 최종 buf 결과인 빈 리스트로 모든 원소가 바뀌어버린다.
순회 중 데이터가 변경되어 나머지 연결된 원소들의 데이터가 변경됨을 막기 위해 generator가 쓰이는데 itertools 모듈의 permutations 함수가 generator를 사용해 구현되어 있다. 원리는 permutation cycle을 활용한다는데 아직은 이해가 잘 안되서 추후에 따로 시간을 들여 정리해보려 한다.
조합 순서쌍 생성하기
조합(Combination)은 서로 다른 n개의 원소에서 r개를 추출하는 방법에 대한 개념이다. 순서를 고려하지 않으므로 순열과는 달리 뽑기만 하면 되겠다.
$\binom{n}{k}=\ _{n}C_{r}=\cfrac{n!}{(n-r)!r!}(0\le r \le n)$
python 코드
def combination(arr, r):
arr = sorted(arr)
result = []
def generate(buf, idx): # idx = 이전 방문 좌표
if len(buf) == r:
result.append(list(buf))
return
for i in range(idx, len(arr)):
buf.append(arr[i])
generate(buf, i + 1)
buf.pop() # backtracking
generate([], 0)
return result
data = "ABC"
for i in range(1, len(data) + 1):
print(["".join(x) for x in combination(data, i)])
data = [1, 2, 3]
print(combination(data, 2))

중복 원소가 존재하는 배열의 순열
중복 원소가 존재할 경우 중복된 순열 순서쌍이 저장될 수 있다. 만약 문제에서 허용된다면 그대로 진행해도 되겠지만 그렇지 않을 경우 set 자료형을 써서 해결해야 한다. 이 문제를 코드로 해결해보자.
위 코드에서 기존 배열을 정렬했으므로 중복 원소는 서로 인접한 상태다. 따라서 버퍼 배열에 원소를 추가할 때 중복 원소를 허용할 지 여부만 체크하면 되겠다.
python 코드
def permutation(arr, r):
arr = sorted(arr, r)
result = []
visited = [0 for _ in range(len(arr))]
def generate(buf):
if len(buf) == r:
result.append(list(buf))
return
for i in range(len(arr)):
if not visited[i] and (i == 0 or arr[i] != arr[i - 1] or visited[i - 1]):
buf.append(arr[i])
visited[i] = 1
generate(buf)
buf.pop()
visited[i] = 0
generate([])
return result
data = "AABC"
for i in range(1, len(data) + 1):
print(["".join(x) for x in permutation(data, i)])
data = [1, 2, 2, 3]
print(permutation(data, 2))
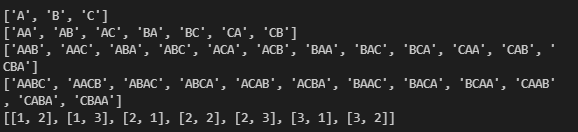
추가된 조건 세 가지의 의미는 다음과 같다.
i == 0: 첫 번째 원소이므로 중복 여부 상관 없음arr[i] != arr[i - 1]: 중복 원소가 아니므로 상관 없음visited[i - 1]: 이미 앞선 글자가 사용된 상태여야 이후 글자에 대해 허용한다. 만약 그렇지 않다면 이미 i - 1번째 글자(동일 글자)에 대한 순회가 모두 끝나 필요가 없는 상태임을 의미하기 때문이다.
중복 원소가 존재하는 배열의 조합
조합의 경우도 순열과 크게 다르지 않다. 중복 원소를 뽑을 경우의 조건만 순열의 경우처럼 체크하면 되겠다.
def combination(arr, r):
arr = sorted(arr)
result = []
visited = [0 for _ in range(len(arr))]
def generate(buf, idx):
if len(buf) == r:
result.append(list(buf))
return
for i in range(idx, len(arr)):
if not visited[i] and (i == 0 or arr[i] != arr[i - 1] or visited[i - 1]):
buf.append(arr[i])
visited[i] = 1
generate(buf, i + 1)
buf.pop()
visited[i] = 0
generate([], 0)
return result
data = "AABC"
for i in range(1, len(data) + 1):
print(["".join(x) for x in combination(data, i)])
data = [1, 2, 2, 3]
print(permutation(data, 2))