힙(Heap)이란?
힙(Heap)은 특성을 만족하는 완전 이진 트리 기반의 자료구조다. 부모노드의 값은 항상 자식 노드의 값보다 크거나(Max heap, 최대 힙) 작아야(Min heap, 최소 힙) 한다. 따라서 루트 노드의 값은 힙 트리의 최소값이거나 최대값이다. 이진트리 기반으로 하는 이유는 다른 구조의 m-ary tree를 사용해도 얻는 이득이 없기 때문이다.
- 힙은 정렬된 구조가 아니다! 따라서 heap에서 자료를 꺼낼 때는 큐처럼 차례로 꺼내야 정렬된 형태의 배열을 얻을 수 있다.
- 힙 정렬, 다익스트라 알고리즘, 최소 신장 트리 등에 사용된다.
힙(Heap) 구현
힙 선언
class BinaryHeap:
def __init__(self):
self.items = [None]
def __len__(self):
return len(self.items) - 1 0번 인덱스를 사용하지 않는 이유는 부모 노드의 각 자식 노드는 부모 노드의 좌표 i에 대해 2i, 2i + 1로 주로 표현되는데 부모 노드의 좌표가 0이 되어버리면 양 자식의 노드 좌표도 0이 되어 탐색이 진행되지 않기 때문이다.
값 삽입
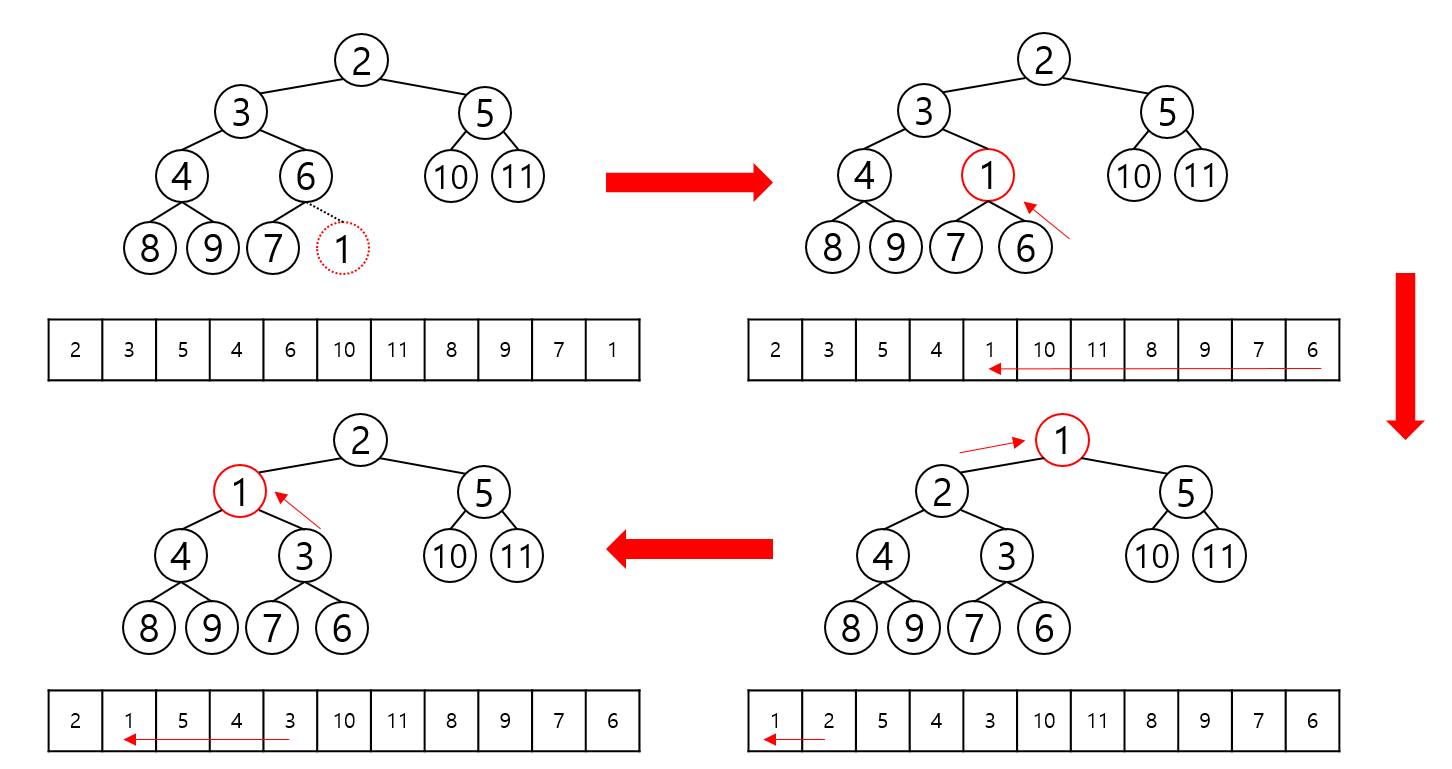
값 삽입은 다음의 순서로 진행된다.
- 삽입될 값은 가장 하위레벨의 최대한 왼쪽에 삽입한다. (가장 끝 자리에 삽입)
- 삽입된 노드와 부모노드의 값과 비교한다.
- 규칙이 성립하면 그대로 두고 위배되면 부모 노드와 값을 바꾼다.
- 이후 규칙이 위배되지 않을 때까지 반복한다.
def insert(self, val):
self.items.append(val)
self._precolate_up()
def _precolate_up(self):
i = len(self)
p = i // 2
while p > 0:
if self.items[i] < self.items[p]: # 최소 힙 조건
self.items[i], self.items[p] = self.items[p], self.items[i]
#if self.items[i] > self.items[p] # 최대 힙 조건
i = p
p = i // 2시간 복잡도는 높이 h만큼이므로 $O(h) = O(log\ n)$이다.
값 추출
루트를 추출하면 힙의 성질에 따라 최소값이나 최대값이 추출된다. 그러나 힙은 정렬된 구조가 아니기 때문에 다시 힙의 성질에 맞춰 재배열하는 "Heapify" 과정이 필요하다.

def extract(self):
extracted = self.items[1]
self.items[1] = self.items[len(self)]
self.items.pop()
self._precolate_down(1)
return extracted
def _precolate_down(self, i):
l, r = 2 * i, 2 * i + 1
t = i
# 최대 힙 조건
# if l <= len(self) and self.items[l] > self.items[target]
# 최소 힙 조건
if l <= len(self) and self.items[l] < self.items[t]:
t = l # 좌측 노드에 대해 검사
if r <= len(self) and self.items[r] < self.items[t]:
t = r # 우측 노드에 대해서도 검사
if t != i: # swap이 요구된다면
self.items[i], self.items[t] = self.items[t], self.items[i]
self._precolate_down(t)전체 코드
class BinaryHeap:
def __init__(self):
self.items = [None]
def __len__(self):
return len(self.items) - 1
def insert(self, val):
self.items.append(val)
self._precolate_up()
def _precolate_up(self):
i = len(self)
p = i // 2
while p > 0:
if self.items[i] < self.items[p]: # 최소 힙 조건
self.items[i], self.items[p] = self.items[p], self.items[i]
# if self.items[i] > self.items[p] # 최대 힙 조건
i = p
p = i // 2
def extract(self):
extracted = self.items[1]
self.items[1] = self.items[len(self)]
self.items.pop()
self._precolate_down(1)
return extracted
def _precolate_down(self, i):
l, r = 2 * i, 2 * i + 1
t = i
# 최대 힙 조건
# if l <= len(self) and self.items[l] > self.items[target]
# 최소 힙 조건
if l <= len(self) and self.items[l] < self.items[t]:
t = l # 좌측 노드에 대해 검사
if r <= len(self) and self.items[r] < self.items[t]:
t = r # 우측 노드에 대해서도 검사
if t != i: # swap이 요구된다면
self.items[i], self.items[t] = self.items[t], self.items[i]
self._precolate_down(t)
heap = BinaryHeap()
nums = [2, 3, 5, 4, 6, 10, 11, 8, 9, 7, 1]
for n in nums:
heap.insert(n)
result = []
for _ in range(len(nums)):
result.append(heap.extract())
print(result)
heap을 빌드하는 과정에서의 엄밀한 시간 복잡도
일반적으로 삽입 과정의 시간 복잡도를 $O(h) = O(log\ n)$이니까 1부터 무한히 발산하는 n에 대해 heap을 build한다고 가정할 때 그 과정의 시간복잡도를 단순히 n을 곱해서 $O(nlog\ n)$이라 표현할 수 있다. 물론 $O(nlog\ n)$보다야 작겠지만 좀 더 엄밀하게 계산하면 $O(2n) = O(n)$이다. 이에 대한 증명 과정은 예전에 작성했던 참고포스트 - Analysis of Algorithms | Time Complexity of building a heap의 좀 더 엄밀하게 계산한 BUILD-HEAP 함수의 시간 복잡도 항목에서 찾을 수 있다.
'Algorithms > Data Structure' 카테고리의 다른 글
| 서로소 집합(Disjoint Set), 유니온 파인드(Union-Find) (0) | 2021.08.02 |
|---|---|
| 트라이(Trie) (1) | 2021.07.05 |
| AVL 트리(Andelson-Velsky and Landis Tree) (0) | 2021.06.29 |
| 이진탐색트리(Binary Search Tree, BST) (0) | 2021.06.28 |
| 트리, 이진트리(Tree, Binray Tree) (0) | 2021.06.27 |