읽기 전
- 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
- 개인적으로 사용해보면서 배운 점을 정리한 글입니다.
그리디 알고리즘(Greedy Algorithm)?
"매 선택마다 현재 시점에서 당장 최적인 답을 선택하여 적합한 결과를 얻는다"는 개념으로 출발하는 알고리즘이다. 즉, 각 단계에서 선택한 결과가 전체적으로도 최선의 결과임을 바라는 알고리즘이다. 다만 그리디 알고리즘이 적용될 수 없는 경우가 있다.
마시멜로 실험을 그리디 알고리즘으로 접근한다고 해보자. 마시멜로 실험에서 지금 당장 1개를 먹거나 지금은 기다렸다가 2개를 먹을 수 있다고 가정할 때, 그리디 알고리즘은 매 순간의 최적해를 구하므로 기다려서 현재 상태가 0이 되는 것보다 먹음으로써 현재 상태를 1로 만드는 것이 최적이라 결정한다.
그리디 알고리즘의 적용 조건
그리디 알고리즘을 적용할 수 있기 위해서 문제는 두 가지 속성을 지녀야 한다.
탐욕 선택 속성(Greedy Choice Priority)
현재의 선택이 이후 선택에 영향을 주지 않음을 의미한다.
최적 부분 구조(Optimal Substructure)
최종 최적 해결 방법이 부분 문제에 대한 최적 해결 방법으로 구성되는 경우를 의미한다.
활동 선택 문제(Acticity Selection Problem)
교실 할당(Classroom Assignment) 문제라고도 부른다. 한정된 공간에서 최대한 많은 수의 수업을 배정해야 한다.

위 그림대로 9개의 수업과 시작 시각 $s_i$와 종료 시각 $f_i$가 주어진다고 하자. 종료 시각이 빠른 순서대로 배치하면 교실의 가용 횟수가 항상 최적이 된다. 종료 시각이 빠르면 종료 시각 이후 뒤의 수업에 영향을 주지 않기 때문이다. 각 수업을 수직선으로 나타내보자.
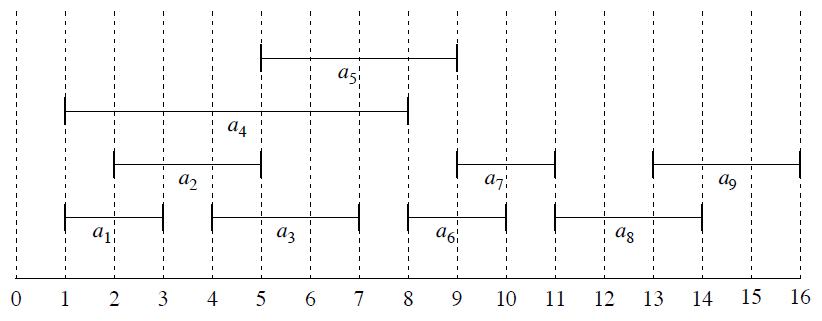
따라서 $a_1,\ a_3,\ a_6,\ a_8$이 최대로 가용할 수 있는 조합이 된다. 시간 측면으로 보면 $a_2,\ a_5,\ a_7,\ a_8$이 12로 최대이지만 마시멜로 실험처럼 $a_1$을 선택하지 않고 $a_2$를 취하는 건 그리디 알고리즘으로 해결할 수 없다. 따라서 선택한 수업들 중 마지막 수업의 종료 시각과 이후 수업의 시작 시각이 겹치는 지 여부만 검사하여 1번의 탐색으로 해결이 가능하기 때문에 시간복잡도는 $O(n)$이다.
python 코드
activity = [[1, 1, 3], [2, 2, 5], [3, 4, 7], [4, 1, 8], [
5, 5, 9], [6, 8, 10], [7, 9, 11], [8, 11, 14], [9, 13, 16]]
sol = []
for act in activity:
if not sol:
sol.append(act)
continue
if act[1] >= sol[-1][2]:
sol.append(act)
print(sol)
'Algorithms > Algorithm' 카테고리의 다른 글
| 다이나믹 프로그래밍(Dynamic Programming, 동적 계획법) (0) | 2021.07.23 |
|---|---|
| 순열, 조합 순서쌍 구현 (0) | 2021.07.22 |
| 이진 탐색(Binary Search) 알고리즘 (0) | 2021.07.10 |
| 카운팅 정렬(Counting Sort, 계수 정렬) 알고리즘 (0) | 2021.07.08 |
| 힙 정렬(Heap Sort) 알고리즘 (1) | 2021.07.08 |