스터디룸

읽기 전

• 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
• 개인적으로 사용해보면서 배운 점을 정리한 글입니다.
• 기술면접만을 준비하기보다 비전공자 입장에서 OS의 기본적인 내용을 짚기 위해 작성되었습니다.

중요도 - 중: 메모리/가상메모리의 페이징과 요구페이징 전반은 물어볼 법하다.

메모리 관리

주소 바인딩

프로세스의 논리적 주소(프로세스의 주소공간)을 물리적 주소로 연결시키는 작업

• 컴파일 타임 바인딩 : 프로그램을 컴파일할 때 결정되는 주소 바인딩 방식
  • 물리적 메모리의 절대 주소로 적재되므로 절대 코드 생성 바인딩 방식이라고도 함
  • 메모리 주소를 변경하려면 재컴파일해야 함
• 로드 타임 바인딩 : 프로그램이 시작될 때 물리적 주소가 결정됨
  • 프로그램에 물리적 메모리 주소 부여를 로더가 책임, 프로그램 종료될 때까지 주소 고정
• 실행시간 바인딩 : 프로그램 실행 후에도 물리적 주소가 변경될 수 있음
  • CPU의 주소 참조 때마다 해당 데이터가 물리적 메모리의 어느 위치에 있는 지 주소 매핑 테이블로 바인딩 체크해야 함
  • 기준 레지스터, 한계 레지스터로 주소 범위를 체크하고 MMU라는 하드웨어 장치 필요
  • MMU기법 : 한계 레지스터로 CPU가 가진 논리적 주소 범위를 체크하고 CPU가 프로세스의 논리적 주소를 가질 때 MMU가 프로세스의 기준 레지스터를 더해 실제 물리적 주소 시작점을 가리킴.

메모리 관리 용어

• 동적 로딩 : 프로세스의 일부만 메모리에 적재하고 실행이 필요할 때만 추가로 적재
• linking : 프로그래머의 소스코드를 컴파일한 결과인 목적파일, 컴파일된 라이브러리 파일을 묶어 실행파일로 만드는 과정
  • 정적 linking : 프로그래머의 코드와 라이브러리의 코드가 합쳐져서 실행 파일 생성
  • 동적 linking : 라이브러리는 제외하며 호출이 되어서야 라이브러리 연결 수행
    • 스텁(stub) : 호출한 라이브러리가 메모리에 존재하는 지 체크. 없으면 디스크에서 동적 라이브러리를 찾아 메모리에 적재함
• 중첩 : 프로세스의 주소 공간을 분할해 실제 필요한 부분만 적재. 동적 로딩과 유사하나 초창기 메모리 자원이 단일 프로세스조차 적재하기 힘들 때 도입되던 개념
• 스와핑 : 중기 스케쥴러에 의해 메모리에서 디스크로 내리거나 그 반대의 과정
  • 컴파일 타임, 로드 타임 바인딩은 물리 주소가 고정되므로 swap-in 시 기존 주소에 적재
  • 스와핑 시간은 디스크 탐색/회전지연 시간보다 실제 데이터 R/W 작업 시간이 주요함
    • 프로세스의 주소 공간이 순차적으로 적재되므로 탐색시간은 적다.

물리적 메모리 할당 방식

• 운영체제 상주 영역 : 인터럽트 벡터, 운영체제 커널 등이 적재된 낮은 주소 영역
• 사용자 프로세스 영역 : 나머지 높은 주소 영역
• 연속할당 방식 : 프로세스를 메모리의 연속된 공간에 적재
  • 고정 분할 : 물리적 메모리를 고정 크기로 사전에 분할하는 방식이다. 각 분할에는 1개의 프로그램만 적재 가능하며 수행 가능한 프로그램 크기에 제약이 발생한다.
    • 외부 조각 : 분할의 크기 < 프로그램 크기로 적재가 불가능해 낭비되는 영역
    • 내부 조각 : 분할의 크기 > 프로그램 크기로 남는 메모리임에도 사용되지 않는 영역
  • 가변 분할 : 적재되는 프로그램에 따라 분할의 크기/개수가 동적으로 변화
    • 프로그램보다 큰 분할은 생성하지 않아 내부 조각(단편화, fragment) 없음
    • 기존 할당된 분할보다 작은 프로그램이 적재되면 나머지 공간에 외부 조각 발생
    • 컴팩션 : 사용 중인 공간을 한쪽으로 몰아 큰 가용 공간 생성. 비용이 많이 들고 물리적 주소 이동이 가능한 실행 시간 바인딩 방식이 지원되어야 함.(외부조각 해결)
    • 동적 메모리 할당 문제 : n크기의 프로세스를 적재할 때 어떤 기준으로 할 지 결정
    • 최초적합 : 가장 먼저 발견되는 가능 공간에 적재. 시간 효율 증가
    • 최적적합 : 가장 n에 가까운 가능 공간에 적재. 공간 효율 증가
• 불연속할당 방식 : 하나의 프로세스를 여러 위치에 분산시켜 할당
  • 페이징 기법 : 동일 크기로 나누어 올림
  • 세그멘테이션 기법 : 의미 단위로 나누어 올림. 크기는 일정하지 않다.
  • 페이지드 세그멘테이션 기법 : 의미 단위로 분할하되 그걸 다시 동일 크기로 분할

페이징 기법

• 프레임 : 물리적 메모리를 페이징과 동일 크기로 분할한 단위.
  • 동적 메모리 할당 문제 해결되었으나 마지막 조각은 내부조각 발생 가능
• 페이지 테이블 : 한 프로세스의 여러 페이지가 물리적 메모리에 혼재되어 있으므로 페이지 별 논리주소를 물리 주소로의 변환을 위한 표
• 페이징의 주소 변환 : CPU의 논리적 주소를 페이지 번호(p), 페이지 오프셋(d)로 나눠서 활용
  • 페이지 번호 : 페이지 테이블의 인덱스, 물리적 메모리 시작 위치를 알 수 있다.
  • 페이지 오프셋 : 페이지 내 변위. 페이지 번호로 찾은 기준 주소 값에 더하면 요청한 논리 주소에 매칭되는 물리 주소를 얻음
• 페이지 테이블 접근 오버헤드 : 페이지 테이블 접근 + 반환된 주소로의 접근 오버헤드
  • TLB : 페이지 테이블 접근 오버헤드를 줄이기 위해 도입된 고속 하드웨어 캐시
    • 가격이 비싸 용량이 작음. 빈번히 참조되는 페이지에 대한 정보만 갖음
    • 요청 페이지 번호가 없으면 페이지 테이블 조회. 있으면 메모리의 프레임으로 직행
    • 문맥 교환 시 TLB 내용도 리셋된다.
  • TLB와 페이지 테이블의 차이점 : 페이지 테이블은 배열과 구조가 유사. TLB는 속도 향상을 위해 연관 레지스터 사용으로 병렬 탐색을 지원하여 동시에 전체 탐색이 가능
  • TLB의 평균 메모리 접근 시간(Effective Access Time:EAT) : 메모리 접근 시간 1, 레지스터 탐색 ε, TLB 존재 확률 α라고 하면 EAT = $(1+\epsilon)\alpha + (2 + \epsilon)(1-\alpha)$=$2+\epsilon-\alpha$
  • $1+\epsilon$은 레지스터 접근 시간과 실제 메모리 접근을 더한 값, $2 + \epsilon$은 TLB에 없어 페이지 테이블에 접근한 시간도 더해진 값이다. ε이 유의미하게 작기 때문에 성능개선이 된다.
• 계층적 페이징 : 프로세스가 요구하는 메모리의 크기가 커짐에 따라 페이지의 수가 많아지고 그에 따른 페이지 테이블의 크기도 과도하게 커진다. 그러나 대부분의 프로그램은 그런 경우가 없어 요구메모리가 큰 프로세스 대응에 공간 낭비 발생을 막기 위해 도입
  • 장점 : 사용되지 않는 공간을 NULL로 표시하여 페이지 테이블에 사용되는 공간 절약
  • 단점 : 주소 변환을 위해 접근하는 페이지 테이블 수 증가로 시간 손해
  • 외부 페이지 테이블 : 논리 주소로부터 다음 페이지 테이블의 주소와 매칭
  • 내부 페이지 테이블 : 마지막 페이지 테이블. 실제 메모리 프레임 주소와 매칭
  • 계층적 페이징의 시간 해결 : TLB를 통해 해결. 4단계 페이징을 예를 들어보자.EAT = $(100 + 20) \cdot 0.9$ + $(500 + 20) \cdot 0.1$ = $160(ns)$으로 시간 부담이 확연히 줄어듬
  • ex) 페이지 테이블 접근 시간 100ns, TLB 접근 시간 20ns, TLB 매칭 확률 90%라 하자.
• 역페이지 테이블 : 물리 메모리의 페이지 프레임 하나씩 항목을 둬서 관리. pid와 페이지 번호가 일치하는 항목의 번호가 실제 프레임의 위치가 됨. 시간 효율 개선을 위해 반드시 연관 레지스터를 사용해야 함.
• 공유 페이지 : 메모리 공간 효율 제고를 위해 프로세스들이 공통으로 공유하는 페이지 운용
  • 공유 코드 : 재진입 가능 코드, 순수 코드라고도 불리며 여러 프로세스에 의해 공통으로 사용되도록 작성된 코드
    • 반드시 읽기 전용이어야 한다.
    • 모든 프로세스의 논리적 공간에서 공유코드는 동일한 위치를 가져야 한다.
  • 사유 페이지/데이터 : 공유 페이지를 제외한 프로세스가 독자적으로 사용하는 공간
• 페이지 테이블의 메모리 보호 : 주소 변환 정보뿐만 아니라 보호비트/유효-무효 비트를 가짐
  • 보호비트 : 각 페이지에 대해 R-W/RO 등의 권한 설정에 사용
  • 유효-무효비트(valid-invalid bit) : 유효라면 해당 메모리 프레임에 페이지 존재, 무효라면 프로세스가 해당 주소를 사용하지 않거나 메모리가 아닌 백킹스토어(스왑영역)에 존재해 해당 프레임에 유효한 접근 권한이 없음을 명시

세그멘테이션

• 세그먼트 테이블 : 주소 변환을 위한 테이블
  • 기준점/한계점 : 물리적 메모리에서의 세그먼트 시작 위치/세그먼트의 길이
• 기준 레지스터/길이 레지스터 : 세그먼트 테이블의 물리적 시작 위치/세그먼트의 개수
• 세그멘테이션의 주소 변환 : CPU의 논리적 주소를 세그먼트 번호/오프셋으로 나눠 관리
  • 세그먼트 번호 : 프로제스 주소 공간에서 몇 번째 세그먼트에 속하는지 표시
  • 오프셋 : 세그먼트 번호에 해당하는 세그먼트 내의 변위 값
  • 세그먼트 번호 > 길이 레지스터 : 존재하지 않는 세그먼트에 대한 접근으로 예외 상황
  • 오프셋 > 한계점 : 세그먼트 범위 초과로 예외 상황
  • 보호비트/유효비트 : 페이징 기법과 동일하나 적용대상이 세그먼트임
• 공유 세그먼트 : 의미 단위로 나뉘어 공유, 보안 측면에서 페이징보다 효과적
  • 사유 데이터가 한 영역에 존재하지 않음(페이징은 한 영역에 존재 가능)
• 크기가 일정하지 않아 가변 분할에서의 문제점을 동일하게 갖음

페이지드 세그멘테이션(Paged Segmentation)

프로그램을 의미 단위인 세그먼트로 분할하되 세그먼트는 동일 크기의 페이지로 재분할

• 세그먼트의 크기는 페이지 크기의 배수
• 페이지트 세그멘테이션 주소 변환 : CPU의 논리적 주소를 세그먼트 번호/오프셋으로 관리
• (외부)세그먼트 테이블 : 세그먼트 길이와 해당 세그먼트의 페이지 테이블 시작 주소를 가짐
• (내부)페이지 테이블 : 각 세그먼트가 갖는 테이블. 물리적 메모리 프레임 위치, 변위값 가짐
  1. 논리 주소의 상위 비트인 세그먼트 번호로 세그먼트 테이블 접근, 해당 항목이 갖고 있는 세그먼트 길이와 오프셋 비교(오프셋 > 길이 : 세그먼트 범위 초과)
  2. 1이 유효하면 오프셋을 페이지 번호와 페이지 오프셋으로 쪼개 페이지 테이블 접근
  3. 페이지 테이블에서 물리적 메모리 프레임 위치와 프레임 내 변위값 찾아 접근

가상 메모리 관리

프로그램이 물리적 메모리를 고려하지 않고 0부터 시작하는 자신만의 메모리를 가정한 공간

• 일부는 물리적 메모리에 일부는 디스크의 스와핑 영역에 존재
• 프로세스의 주소 공간을 메모리로 적재하는 기법 : 단위에 따라 요구 페이징/ 세그멘테이션

요구 페이징

당장 사용할 페이지만을 올려두고 CPU의 요청에 따라 보조기억 장치의 swap 영역에서 로드해 메모리에 적재한다.

• 물리적 메모리 용량 제약을 벗어나게 하는 효과
• 모든 프로그램은 자신만의 가상 메모리 주소를 갖고 OS는 이 가상 메모리 주소를 물리적 주소로 매핑하는 기술을 사용해 주소를 변환 후 물리적 메모리에 프로그램을 적재
• 프로그램의 크기가 크더라도 모든 요소가 동시에 사용되진 않는다는 점을 참고하여 현재 사용 중인 크기만 적재하고 나머지는 보조기억 장치에 저장했다가 필요할 때 적재
• 페이징 테이블에 유효-무효 비트를 둬서 메모리 적재 여부 체크
  • 프로세스 시작 전에는 모든 페이지의 유효-무효 비트값은 무효. 적재 시 valid로 변경
  • swap out될 valid에서 invalid로 변경
• 페이지 부재(fault) : 페이지가 메모리에 없어 무효로 마킹된 상태
• 요구 페이징의 page fault 처리
  1. 주소 변환을 담당하는 MMU가 page fault trap 발생
  2. CPU의 제어권이 커널 모드로 이양, page fault 처리루틴 수행. 적법하면 물리적 메모리에 빈 프레임을 할당 받아 해당 페이지를 load
     • 빈 프레임이 없으면 적재된 페이지 중 하나를 swap-out
     • swap-in은 소요시간이 길어 페이지 부재 발생 프로세스 봉쇄로 전환 - PCB에 저장
     • swap-in 완료 시 인터럽트 발생, 유효비트 valid 마킹, 프로세스 준비 큐로 이동
  3. 해당 페이지의 접근의 적법 여부 체크. 위반 시 프로세스 종료
• 요구 페이징의 성능 : page fault 발생 빈도가 가장 큰 영향(swap-in 때문)
  • 유효 접근시간 : 요청한 페이지를 참조하는 데 걸리는 시간. (P = page fault rate)
    1. $(1 - P)$ * 메모리 접근 시간
    2. P * 페이지 부재 발생 처리 오버헤드
    3. P * 빈 프레임이 없을 경우 swap-out 오버헤드 + 요청 페이지의 swap-in 오버헤드
    4. P * 프로세스의 재시작 오버헤드
       유효 접근시간의 계산은 위 4개의 값을 더한 결과다.

페이지 교체

• 전역 교체 : 교체 알고리즘의 대상이 모든 페이지 프레임인 경우
• 지역 교체 :교체 알고리즘을 프로세스 별로 독자적으로 적용
• 교체 알고리즘 : swap-out할 시 어떤 프로세스에 수행할 지 결정하는 알고리즘
  • page falut rate 최소화가 목적
  • 페이지 참고열에 대해 page fault rate를 계산하여 성능 평가
• 최적 페이지 교체 - MIN, OPT
  • 가장 최적의 알고리즘, 미래의 페이지 참조를 알고 있어 실제 적용은 안됨
  • 성능 평가의 상한선
  • 가장 먼 미래에 참조될 페이지를 swap-out하면 된다.
• FIFO(First In Fist Out)
  • 향후 참고 가능성 고려 없이 물리적 메모리에 들어온 순서대로 swap-out
  • 단점 : 먼저 진입한 페이지의 참조가 계속 빈번하면 page fault도 빈번히 발생
  • FIFO 이상현상(anomaly) : 메모리를 증가시켰음에도 page fault가 증가
• LRU(Least Recently Used)
  • 시간 지역성(temporal locality) : 최근 참조된 페이지는 다시 참조될 가능성이 높다.
  • 마지막 참조 시점이 가장 오래된 페이지는 swap-out
• LFU(Least Frequently Used)
  • 물리적 메모리에 적재된 페이지들 중 과거 참조 횟수가 가장 적은 페이지 swap-out
    • 여러 개라면 그들 중 더 오래된 페이지 swap-out이 바람직
  • Incache-LFU : 메모리에 적재된 순간부터 count, swap-in되면 1부터 다시 count
  • Perfect-LFU : 메모리 적재 여부와 상관없이 count, 오버헤드가 크다.
  • 장점 : LRU보다 장기적인 기록 반영 가능
  • 단점 : 시간에 따른 참조변화 반영 불가능. LRU보다 구현이 어려움. 특정 페이지를 집중적으로 사용하다 계속 적재될 경우 불필요하게 상주할 수 있음
• 클럭
  • LRU/LFU가 참조시각, 횟수를 소프트웨어적으로 유지,비교를 요구하여 오버헤드 발생
  • 하드웨어 장치를 둬서 오버헤드 감소, 대부분의 시스템에서 도입
  • LRU 근사 알고리즘으로 NUR(Not Used Recently), NRU(Not Recently Used)로도 부름
  • 오랫동안 참조되지 않은 페이지 중 하나를 교체, LRU와 달리 교체된 페이지가 가장 오래 전에 참조된 페이지임을 보장하지 않음
  • 페이지 프레임의 참조 비트를 조사
    • 프레임의 페이지 참고 시 참조 비트를 1로 마킹
    • 클럭 포인터가 지나갈 때 1로 마킹된 항목은 0으로, 이미 0인 경우는 swap-out
    • 최초 참조 이후 1번의 기회를 준다는 의미로 2차 기회 알고리즘으로도 부름

페이지 프레임의 할당

• 할당 알고리즘 : 프로세스가 여러 개 수행될 때 각 프로세스의 메모리 할당 크기를 결정한다.
  • 균등 할당 : 모든 프로세스 동일 프레임 할당
  • 비례 할당 : 프로세스 크기에 맞춰 할당
  • 우선순위 할당 : 당장 CPU에 실행될 프로세스와 그렇지 않은 프로세스 구분하여 할당

스레싱(thrashing)

집중적으로 사용되는 페이지들을 한번에 적재하지 못해 page fault rate가 크게 상승하여 CPU 이용률이 급격하게 감소하는 현상

• MPD(Multi-Processing Degree, 다중 프로그래밍 정도) : 메모리에 동시에 적재되어 있는 프로세스의 수

1. OS는 CPU 이용률이 낮으면 MPD가 적다고 해석
   • 준비 큐가 비어있는 경우 MPD가 적어 이들이 모두 I/O 작업 중이라 판단하여 MPD를 증가시키려고 함
2. MPD 과도하게 증가 시 프로세스 할당 메모리가 급격히 감소하여 페이지 부재 빈번히 발생
   • 빈번한 페이지 부재 처리로 swap-in 계속 발생하여 CPU 이용률 감소
3. 1-2를 순환하며 악순환 발생 - 대부분의 시간에 CPU가 일을 안함

• 스레싱 방지 알고리즘 : MPD를 적절히 조절하는 알고리즘
  • 워킹셋 알고리즘 : 지역성 집합이 메모리에 동시에 적재되도록 보장
    • 지역성 집합 : 일정 시간 집중적으로 참조되는 페이지 집합
    • 워킹셋 : 한 번에 메모리에 적재되어야 하는 페이지들의 집합
    • 워킹셋을 구상하는 페이지들이 한번에 적재가능한 경우에만 메모리 할당
    • 적재가 불가능하면 전체 반환 후 swap-out
    • 워킹셋 윈도우 : 워킹셋 생성을 위해 사용하는 윈도우. 너무 크면 지역성 집합은 많이 수용하나 MPD 감소, 너무 작으면 지역성 집합을 모두 수용하지 못함
      아래 그림은 워킹셋 알고리즘의 작동 도식이다. 워킹셋 윈도우에 포함되는 페이지 참조 빈도에 따라 워킹셋 집합의 크기도 조절되어 동적으로 프레임 할당 기능까지 수행

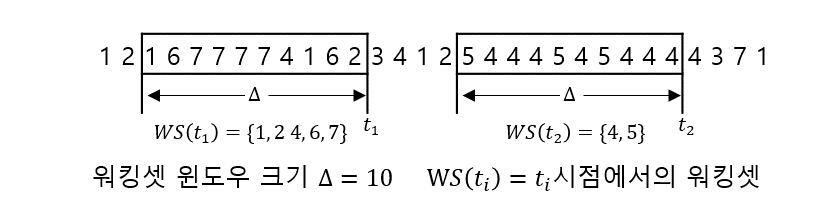
• 페이지 부재 빈도(Page Fault Frequency: PFF) 알고리즘 : 프로세스의 부재율을 주기적으로 조사한 뒤 각 프로세스에 할당할 메모리 양 동적으로 조절
  • 프로세스 페이지 부재율 > 상한값 : 프로세스에 할당된 프레임 부족 간주, 빈 프레임 없으면 swap-out하여 MPD 감소
  • 프로세스 페이지 부재율 < 하한값 : 프로세스에 필요 이상의 프레임 할당 간주, 할당된 프레임 감소
  • 위 방식대로 할당했음에도 프레임이 남으면 swap-in하여 MPD 증가

웹캐싱 기법

컨텐츠 전송 네트워크(Contents Delivery Network: CDN) 서비스 활성화로 원격지의 객체를 캐싱하여 사용자가 인터넷 정보에 신속한 접근이 가능하게 함을 목적으로 한다. 웹 사용자에 의해 빈번히 요청되는 데이터를 웹캐시 서버에 보관해 빠른 서비스를 가능하게 하는 기법

• 프락시 서버 : 웹 사용자의 서비스 지연시간 감소를 목적으로 도입, 네트워크 대역폭 절약과 웹서버 부하 감소 역할
• 역방향 프락시 캐시 : 웹서버에 도입되는 개념으로 특정 그룹의 웹서버 객체들을 캐싱하여 서버 부하를 직접적으로 줄이고 사용자의 지연시간도 감소시킴
• 캐시 교체 알고리즘 : 한정된 캐시 공간으로 인해 어떤 객체를 캐시에 보관/삭제할 지 온라인으로 결정
• 일관성 유지 : 근원지 서버의 웹 객체가 변경될 수 있어 캐싱된 객체가 최신인지 체크 후 사용자에게 최신상태 전달

웹캐시 교체 알고리즘

페이징 기법은 객체의 크기가 동일해 캐시부재(cache miss) 발생 시 로딩 비용이 균일하나 웹캐싱은 근원지 서버의 위치/특성에 따라 비용이 다르고 파일 단위의 캐싱이기에 캐싱 단위도 균일하지 않아 객체의 이질성을 고려해야 한다.

• 교체 알고리즘의 성능 평가 : 객체 i에 대해 $c_i$는 인출비용, $r_i$는 총 참조횟수, $h_i$는 캐시 적중횟수, $s_i$는 객체의 크기, $d_i$는 서버로부터의 인출 지연시간이라 하자.

  • 캐시 적중률(Hit Rate: HR) : 전체 요청 중 캐시에 적중되어 서비스된 요청의 비율 ($\cfrac{\sum{h_i}}{\sum{r_i}}$)
  • 비용 절감률(Cost-Savings Ratio: CSR) : 객체의 이질성을 고려한 비용까지 계산에 포함 ($\sum c_i \cdot \cfrac{h_i}{r_i}$), $c_i$ 정의 방식에 따라 CSR은 BHR이나 DSR이 될 수 있다.
    • 바이트 적중률(Byte Hit Rate: BHR) : $\sum s_i \cdot \cfrac{h_i}{r_i}$
    • 지연 감소율(Delay Savings Ratio: DSR) : $\sum d_i \cdot \cfrac{h_i}{r_i}$

• 참조 가능성의 예측

• 

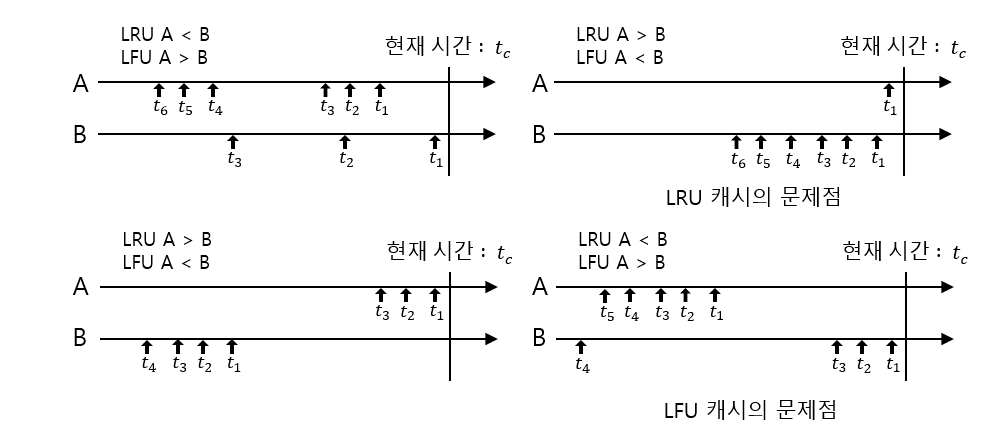
  • 아래 그림처럼 LRU, LFU는 성격에 따라 문제가 발생하는 케이스가 존재한다.
  • 시간 지역성과 최근 참조빈도(인기도)를 고려함이 바람직하다.
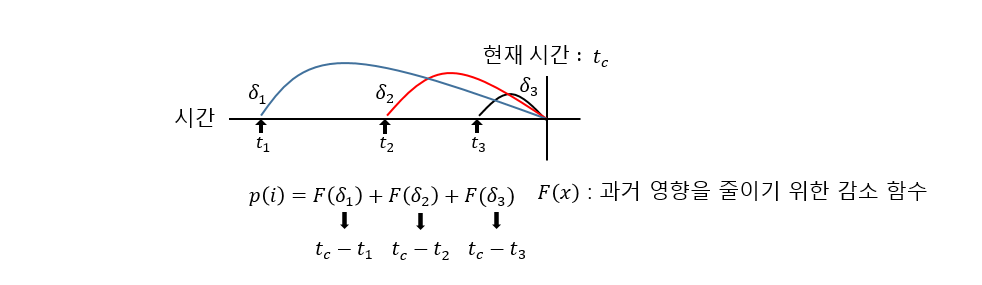
  • LRFU(Least Recently Frequently Used) : 객체의 참조 가능성 계산 시 과거 참조 시점과 횟수 이용
    • 시점 $t_c$에서의 객체 i의 참조 가능성 $P(i)=\sum_{k=1}^{n}F(t_c - t_n)$이다.
    • F(x)는 감소함수이고 $(\cfrac{1}{2})^{\lambda x}\ (0\le \lambda \le 1)$로 정의
    • $\lambda = 1$이면 $2^n\ge \sum_{i = 1}^{n - 1} 2^i$에 따라 최근값만 반영되어 LRU로 동작
    • $\lambda = 0$이면 고정값으로 LFU로 동작

• 인기도를 반영할 때 노화(aging)기법을 적용해 캐시 오염 방지

  • 캐시 오염 : 과거 참조가 많았다는 이유로 최근까지 불필요하게 유지된 상태

• 객체의 이질성 고려

  • 캐시 적중률과 적중했을 때 절약되는 비용을 동시에 고려해야 함
  • 대부분 알고리즘은 비용절감률이 최대 목적

• 캐시 교체 알고리즘의 시간복잡도

  • 수십/수백만 개의 객체로 인해 적어도 $O(log\ n)$을 넘지 않아야 한다.
  • LRU 캐시 알고리즘 : O(1), 이질성고려 X, 인기도 고려 X
  • 대부분 힙 자료구조를 사용해 $O(log\ n)$으로 해결한다.

웹캐시의 일관성 유지 기법

• 약한 일관성 유지 : 캐싱된 객체가 변경되었을 가능성이 높은 경우에만 확인
  • adaptive TTL : 객체의 최종 변경 시각과 최종 확인 시각을 고려하여 가능성 계산
    • LMF로 판단하여 임계값 이상일 경우 근원지 서버에 확인 요청
    • $LMF = \cfrac{C-V}{V-M}$ (C: 현재 시각, V: 최종 확인 시각, M: 최종 변경 시각)
• 강한 일관성 유지 : 반드시 최신 정보를 사용자에게 보장하기 위해 일일히 확인
  • 일반적으로 오버헤드를 고려하여 약한 일관성 유지기법 채택
  • polling-every-time : 객체에 대한 요청이 들어올 때마다 근원지 서버에 확인
  • invalidation : 자신의 객체를 캐싱하는 모든 프락시 서버를 기록, 객체가 변경될 경우 통지

웹캐시의 공유&협력 기법

• ICP(Internet Cache Protocol) : 프락시 캐시들 간 웹객체의 검색/전송 지원
  • cache miss 발생 시 동료 프락시에 ICP 질의를 멀티캐스트, 다른 캐시가 보유한 상태면 HTTP 요청 전송

웹캐시의 사전확인

• 웹캐시의 사전인출(Prefetching) : 웹 서비스의 응답 지연시간 감소를 위해 사용자가 아직 요청하지 않은 객체를 미리 받아오는 방식
  • 예측 사전인출 : 웹페이지들 간 관계그래프 등을 구성해 참조될 확률 계산하여 사전인출 수행
  • 대화식 사전인출 : 사용자가 HTML 문제에 대한 요청 시 HTML 코드 파싱하여 포함/연결된 웹 객체 사전인출
• 웹캐시의 유효성 사전확인 : 캐싱된 객체 참조 확률을 계산하여 미리 유효성을 확보, 요청 시 확인작업 없이 전송

관련 포스팅

1. 기술면접을 위한 OS 개념정리 01 - CPU 스케쥴링, 입출력 관리, 디스크 관리

2. 기술면접을 위한 OS 개념정리 02 - 프로세스, 스레드

3. 기술면접을 위한 OS 개념정리 04 - 프로세스 동기화, 데드락

읽기 전

• 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
• 개인적으로 사용해보면서 배운 점을 정리한 글입니다.
• 기술면접만을 준비하기보다 비전공자 입장에서 OS의 기본적인 내용을 짚기 위해 작성되었습니다.

중요도 - 최상: OS가 기술면접에 나온다면 태반은 프로세스/스레드 관련이다.

프로그램의 구조와 동작

• 프로그램 : 작업을 위해 실행할 수 있는 파일
• 프로그램 카운터(Program Counter, PC) : CPU가 매 시점마다 메모리의 특정 주소의 명령을 하나씩 읽어와 실행하는 데 이 때 CPU가 수행해야 할 메모리 주소를 담고 있는 레지스터이다. 조건문/반복문/함수 호출로 인한 주소 이동이 없다면 프로그램 카운터는 항상 다음 명령어를 가리켜서 코드를 순차적으로 수행한다.
  • 메모리에는 사용자 프로그램과 운영체제가 같이 적재되어 수행된다. 프로그램 카운터가 운영체제가 위치한 부분을 가리키면 커널 모드에서 명령을 수행 중이고 사용자 프로그램 주소를 가리키면 사용자 모드에서 CPU가 사용자 프로그램을 수행하고 있다고 말할 수 있다.
• 프로그램의 실행 : 디스크의 실행 파일이 메모리에 적재됨과 프로그램이 CPU를 할당받고 명령을 수행하고 있는 상태를 의미한다.

프로세스와 스레드

• 프로세스 : 운영체제로부터 시스템을 할당받는 작업의 단위, 동적인 개념으로 현재 실행 중인 프로그램이다.
  • 기본적으로 최소 1개의 스레드(메인 스레드)를 갖는다.

프로세스 구조

• 프로세스의 주소 공간 / 가상 메모리 / 논리적 메모리 : 실제 메모리 주소와 독립적으로 각 프로그램마다 독자적인 주소 공간을 갖기에 가상 메모리, 논리적 메모리라고도 부르며 코드(code), 데이터(data), 스택(stack), 힙(heap) 등으로 구성된다.
  • 코드 영역 : 사용자가 작성한 프로그램 함수들의 코드가 CPU에서 수행할 수 있는 기계어 명령 형태로 변환되어 저장되는 부분
  • 데이터 영역 : 전역 변수 등 프로그램이 사용하는 데이터를 저장하는 부분
  • 스택 영역 : 함수가 호출될 때 호출된 함수의 수행을 마치고 복귀할 주소 및 데이터를 임시로 저장하는 공간이다.
  • 운영체제 역시 프로그램이므로 운영체제 커널도 프로세스 주소 공간을 갖는다.
    • 커널의 코드 영역 : CPU와 메모리 관리, 인터페이스 제공 코드 등이 주를 이룬다.
    • 커널의 데이터 영역 : 자원을 관리하기 위한 자료구조를 저장한다.
    • 커널의 스택 영역 : 함수 호출 시 복귀 주소를 저장하기 위한 용도는 맞지만 사용자 프로그램이 시스템 콜을 하여 커널 함수로 접근 시 상황을 고려하여 일관성 유지를 위해 프로세스마다 별도의 스택을 둔다.
      • 일반 프로그램이 시스템 콜을 할 때 CPU의 수행 주체가 프로그램에서 OS로 전환되며 PCB에 일반 프로그램 복귀 정보를 저장한다.
      • 커널 스택에 일반 프로그램에 대한 별도의 스택을 두어 관리한다.
• 힙 영역 : 동적으로 할당되는 데이터들을 위해 존재하는 공간 (new(), mallock() 등)
• PCB : OS가 프로세스를 표현하는 개체. 문맥교환 시 PCB와 TCB를 모두 저장한다.
• 프로세스의 두 가지 실행 상태
  • 사용자 모드에서의 실행 상태(user mode running) : 자신의 주소 공간에 정의된 코드를 실행
  • 커널 모드에서의 실행 상태(kernel mode running) : 시스템 콜 함수를 실행
    • 시스템 콜을 하여 실행되는 코드가 커널의 코드라 할 지라도 커널은 호출 프로세스의 일을 대행할 뿐이므로 요청 프로세스 A가 여전히 실행 상태에 있다고 간주하며 단지 코드 실행 주체를 구분짓기 위해 두 가지로 나눈 것이다.

스레드 구조

• 스레드 : 프로세스가 할당받은 자원을 이용하는 실행 흐름의 단위. 프로세스의 특정한 수행 경로이다.

• 프로세스 주소공간 내에서 각각 stack만 따로 할당 받으며 별도의 PC 레지스터를 갖는다.
• 프로세스의 주소공간(코드, 데이터)이나 자원(힙 영역)을 같은 프로세스의 스레드끼리 공유하며 힙 메모리에 서로 읽고 쓰기 작업을 수행한다.
• 한 스레드가 프로세스 자원 변경 시 다른 스레드도 그 변경 결과를 즉시 확인 가능하다.
• TCB : PC 레지스터, CPU 정보, PCB 포인터를 갖는다. 스레드끼리의 문맥 교환 시 TCB만 저장한다.
• Java에서의 스레드 : 일반 스레드와 차이는 거의 없고 JVM이 OS의 역할을 수행한다.
  • Java에선 프로세스가 존재하지 않고 스레드만 존재하며 스레드의 스케쥴링은 JVM이 책임진다.
  • OS에서의 프로세스가 Java에서는 스레드처럼 간주되어 OS가 관리하던 프로세스 수, 메모리 위치, 프로세스의 상태, 우선 순위 등이 전부 스레드로 바뀌어 JVM이 관리한다.
  • 개발자는 스레드로 동작할 코드를 작성해 JVM이 스레드를 실행하도록 요청

멀티 프로세스, 멀티 스레드 등 다중처리

• 멀티 프로세스 : 하나의 프로그램을 여러 프로그램으로 구성하여 각 프로세스가 하나의 작업 처리(병렬 처리)
  • 장점 : 자식 프로세스 중 하나에 문제가 발생해도 다른 프로세스에는 영향이 없어 안정성이 높다.
  • 단점
    • 문맥 교환에서의 오버헤드 : 캐시 메모리 리셋 등 무거운 작업 발생
    • 프로세스 간 복잡하고 어려운 IPC : 독자적인 메모리 공간으로 변수 공유가 안됨
• 멀티 스레드 : 하나의 프로세스에 여러 스레드로 자원을 공유하며 작업을 나누어 수행
  • 장점
    • 일부 스레드가 중단되거나 긴 작업을 수행해도 프로그램 동작이 계속되어 사용자와의 응답성 증가
    • 시스템 자원의 효율성 증가 : 단일 스레드와 비교할 때 프로세스 생성 시 자원을 할당하는 시스템 콜 감소
    • 처리 비용 감소 : 코드, 데이터, 힙을 공유하기에 다른 스레드들 간의 공유가 쉽다.
    • 문맥 교환 비용 감소 : 캐시 메모리를 비울 필요가 없어 비교적 가벼운 TCB만 전환하면 된다.
  • 단점
    • 자원을 공유함에 따라 동기화 문제 발생 가능(병목 현상, 데드락)
    • 과도한 동기화 과정으로 인해 성능 저하 가능성이 있음
    • 하나의 스레드의 문제로 예외상황 등 발생 시 전체 프로세스에 영향을 주거나 아예 종료될 수 있다.
    • 단일 프로세스 환경에서는 효과가 저하되어 스레드 생성시간으로 인해 단일 스레드보다 느리다.
• 멀티 코어 : CPU 내부에 레지스터와 캐시를 갖는 코어만 따로 회로를 구성
• 멀티 프로그래밍 - 멀티 태스킹
  • 멀티 프로그래밍 : 하나의 메모리에 동시에 여러 프로세스를 적재
  • 멀티 태스킹 : 멀티 프로그래밍된 메모리에 대해 CPU가 시분할로 여러 프로세스를 concurrency하게 처리함(concurrency : 동시에 처리되는 것처럼 보임)

프로세스 관리

• 프로세스의 문맥(context) : 프로세스가 어떤 상태에서 수행되고 있는지 규명하기 위해 필요한 정보
  • 하드웨어 문맥 : CPU의 수행 상태를 기록. 프로그램 카운터 값, 레지스터에 저장된 값
  • 프로세스의 주소 공간 : 코드/데이터/스택으로 구성된 독자적인 주소 공간
  • 커널 상의 문맥 : 프로세스를 관리하기 위한 자료구조를 취급. PCB, 커널 스택 등이 있음
• 프로세스의 상태 : 기본적으로 실행, 준비, 봉쇄 세가지로 구분되나 시작, 완료, 정지도 있음
  • 실행(running) 상태 : 프로세스가 CPU를 할당받아 기계어 명령을 수행 중인 상태
  • 준비(ready) 상태 : CPU만 할당받으면 명령 수행이 가능하지만 아직 못 받은 상태
  • 봉쇄(blocked) 상태 : CPU를 할당받아도 당장 명령을 실행할 수 없는 상태
  • ex) 프로세스가 요청한 입출력 작업을 진행하고 있는 경우
  • 시작(new) 상태 : 프로세스가 생성되어 프로세스를 위한 자료구조는 있으나 메모리 획득 권한을 아직 받지 못한 상태
  • 완료(terminated) 상태 : 프로세스는 종료되었으나 OS가 프로세스와 관련된 자료구조를 아직 정리하지 못한 상태
  • 중지(suspend) 상태 : 중기 스케쥴러의 등장으로 새로 도입된 개념. 메모리 공간을 위해 메모리를 빼앗겨 디스크의 스왑 영역으로 옮겨진 상태 - 아래에서 다시 다룸

• 문맥 교환(context switch) : 기존 수행 중인 사용자 프로세스의 문맥을 저장하고 새로운 사용자 프로세스의 문맥을 세팅하여 CPU 제어권을 넘기는 과정
  • 프로세스가 교체될 경우 PCB와 TCB를 교환하지만 멀티 스레드 환경에서 스레드의 문맥교환은 TCB만 교환되어 오버헤드가 비교적 적다. (문맥 교환의 기본 단위는 TCB)
  • 기존 할당 프로세스 : 프로세스의 문맥을 PCB에 저장
  • 신규 할당 프로세스 : 프로세스의 문맥을 PCB로부터 실제 하드웨어로 복원
  • 시스템 콜이나 인터럽트 처리로 인해 CPU의 제어권을 OS로 넘기는 행위는 문맥 교환으로 간주하지 않는다. 프로세스의 실행 모드가 바뀔 뿐 시스템 콜/인터럽트 처리가 끝나면 마저 기존 프로세스로 복귀하여 수행하기 때문이다.
• CPU 디스패치(dispatch) : 준비 상태의 프로세스 중 CPU를 할당받은 프로세스를 선택해 제어권을 넘기는 과정
• ex) 타이머 인터럽트나 실행 중인 프로세스의 입출력 요청으로 인한 봉쇄 상태 전환 시 발생

프로세서 제어 블록 - PCB, 스레드 제어 블록 - TCB

• PCB에 저장되는 정보
  • 프로그램 카운터의 값 : 다음에 실행할 명령어의 주소- 단일 스레드, 멀티 프로세스 환경
  • CPU 레지스터의 값 : CPU 연산을 위해 현재 레지스터의 저장 값을 나타냄- 단일 스레드, 멀티 프로세스 환경
  • 프로세스의 상태 : CPU 할당 여부 결정에 필요 - new, ready, waiting 등의 상태 저장
  • CPU 스케쥴링 정보 : 프로세스의 우선순위, 스케쥴 큐에 대한 포인터 등을 저장
  • 메모리 관리 정보 : 페이지 테이블, 세그먼트 테이블 등의 메모리 할당 관련 저장
  • 입출력 상태 정보 : 프로세스에 할당된 입출력 장치와 열었던 파일 정보 저장
  • 자원 사용 정보 : 사용된 CPU 시간, 시간 제한, 계정 번호 등 저장
• TCB에 저장되는 정보
  • 프로그램 카운터 값 : 다음에 실행할 명령어의 주소 - 멀티 스레드 환경
  • CPU 레지스터의 값 : CPU 연산을 위해 현재 레지스터의 저장 값을 나타냄 - 멀티 스레드 환경

프로세스의 스케쥴링

큐는 각 프로세스의 PCB를 연결리스트로 관리한다.

• 준비 큐 : CPU를 할당받기 위해 다기 중인 준비 상태의 프로세스들을 담는다.
• 장치 큐 : 장치 별로 특정 자원을 기다리는 프로세스들을 담은 큐. 동기성을 보장하며 장치 큐에 속한 프로세스는 봉쇄 상태이다.
• 작업 큐 : 준비 큐, 장치 큐의 모든 프로세스는 작업 큐에 속한다. 모든 프로세스를 관리.
• 스케쥴러 : 어떤 프로세스에게 자원을 할당할 지 결정하는 OS 커널의 코드
  • 장기 스케쥴러(Long-term scheduler, job scheduler)
    • 메모리와 디스크 사이의 스케쥴링 담당
    • 프로세스에 메모리 및 각종 리소스 할당(admit)
    • degree of Multiprogramming(실행 중인 프로세스의 수) 제어
    • 메모리에 너무 많은 프로세스가 적재되면 CPU 수행에 필요한 데이터를 적재하지 못해 디스크로 빈번하게 요청하여 인터럽트가 수시로 발생
    • 프로세스의 상태를 new에서 ready로 전환하며 현대 시분할 시스템에서는 메모리가 충분해 잘 쓰이진 않는다.
  • 어떤 프로세스를 준비 큐에 넣을 지 결정하여 프로세스의 상태를 시작에서 준비로 바꾼다. 프로세스가 CPU에서 실행되기 위해선 메모리를 가져야하기 때문이다.
  • 단기 스케쥴러(Short-term scheduler, CPU scheduler)
    • CPU와 메모리 사이의 스케쥴링 담당
    • 준비 큐에 있는 프로세스 중 실행으로 바꿀 프로세스 결정
    • 프로세스에 CPU 할당
    • 시분할 시스템의 타이머 인터럽트 발생 시 단기 스케쥴러가 호출된다.
  • 중기 스케쥴러(Medium-term scheduler, Swapper)
    • 메모리 공간 확보를 위해 프로세스를 메모리에서 디스크로 보내버림(swapping)
    • 프로세스에 할당된 메모리를 deallocate
    • degree of Multiprogramming 제어
    • 프로세스의 상태를 준비에서 정지(suspend)로 전환
  • 메모리 자원이 충분해져 장기 스케쥴러의 효용이 떨어지자 등장한 개념
  • 스왑 아웃(swap out) : 중기 스케쥴러에 의해 메모리에 적재된 프로세스의 메모리를 빼앗고 그 내용을 디스크 스왑 영역에 저장하는 행위
  • 중지 상태 : 중기 스케쥴러에 의해 프로세스가 스왑 아웃된 상태
    • 중지준비 : 준비 상태의 프로세스가 스왑 아웃
    • 중지봉쇄 : 봉쇄 상태의 프로세스가 스왑 아웃, 봉쇄가 끝나면 중지준비로 변경

프로세스의 생성

최초의 프로세스는 OS가 생성하고 이후는 각 프로세스가 다른 프로세스를 생성한다.

• 부모/자식 프로세스 : 프로세스를 생성한 프로세스 / 프로세스로부터 생성된 프로세스
  • 프로세스의 생성 이후 : 부모는 자식의 수행이 완료될 때까지 봉쇄되거나 같이 수행되며 CPU 점유율 경쟁
  • 프로세스의 종료 : 모든 자식 프로세스가 종료된 뒤에야 부모 프로세스가 종료됨
  • 자식 프로세스 주소 공간 : 부모 프로세스의 주소 공간의 내용을 그대로 복제한 뒤 덮어씌우며 프로그램 수행
  • 로그아웃 이후 자식 프로세스 유지 : 로그인 하단에서 생성한 자식 프로세스를 로그아웃 이후에도 유지하고 싶을 경우 로그아웃 후에도 유지되는 부모 프로세스에게 이양 후 로그인 하단의 프로세스를 종료한다.
  • 생성된 자식 프로세스의 실행 : 부모 프로세스의 주소공간을 복제함에 따라 부모가 수행한 지점(프로그램 카운터 지점)에서 시작된다. 다만, 부모에게 프로세스 복제 결과값을 1로, 자식에겐 0을 주어 자신이 복제본임을 구분하게 한다. 이후 부모의 복제된 내용과 다른 프로그램을 수행하기 위해 별도의 실행 함수를 호출하여 주소 공간을 덮어 씌운다.
  • 부모와 자식의 동기화 : 실행 후 서로 경쟁하지 않고 자식의 결과를 받아서 사용해야 하면 부모는 wait() 호출하여 봉쇄상태에 두고 자식 종료 후에 부모를 준비 큐에 넣는다.

프로세스 간 통신

• IPC(Inter-Process Communication) : 실행 중인 다른 프로세스 간 발생하는 통신이며 의사소통 기능과 동기화를 보장하기 위한 매커니즘이다.
  • 메세지 전달 : 프로세스 간 공유 데이터 없이 메세지를 주고받아 통신
    • send&receive : OS의 시스템 콜 함수
    • 직접 통신 : 두 프로세스 간 직접 통신한다. 통신하려는 프로세스를 명시적으로 표시하며 두 프로세스 간에는 오직 1개의 커뮤니케이션 링크만 존재한다.
      • 익명 파이프 : 단방향 파이프로 한 쪽은 전송만, 한쪽은 수신만 가능
        • 장점 : 사용이 매우 간단하므로 단순 데이터 흐름에서는 효율적임
        • 단점 : 양방향 통신에서는 파이프 2개가 필요하므로 구현이 어려움
      • 기명(named) 파이프 : 익명 파이프와 같이 반이중 통신 파이프로 이름이 있는 파일을 사용한다.
        • 장단점은 익명 파이프와 동일
    • 간접 통신 : 메일 박스나 포트로부터 메세지를 송/수신한다. 각 메일 박스의 고유한 ID를 공유하는 프로세스들끼리만 메세지를 전달한다. 송신자가 메일 박스로 메시지 전달 후 메일 박스가 수신자에게 메세지(공유하고자 하는 데이터의 메모리 주소) 송신, 수신자 특정은 링크(메일박스) 할당 등의 방법으로 해결한다.
      • 메시지 큐 : 메일박스(1개만 전송)의 배열 형태로 구성, 데이터의 흐름이 아닌 메모리 공간이다.
  • 공유 메모리 : 프로세스들이 주소 공간의 일부를 공유한다. 원칙적으로 개별 공간이지만 시스템 콜로 공유를 지원한다. 물리적 메모리에 매핑 시 공유 메모리 주소 영역은 A, B 프로세스가 서로 같은 주소에 매핑된다.
    • 동기화 문제 : 커널이 책임지지 않으므로 프로세스들끼리 직접 해결해야 한다.

관련 포스팅

1. 기술면접을 위한 OS 개념정리 01 - CPU 스케쥴링, 입출력 관리, 디스크 관리

2. 기술면접을 위한 OS 개념정리 03 - 메모리, 가상 메모리 관리, 웹캐싱 기법

3. 기술면접을 위한 OS 개념정리 04 - 프로세스 동기화, 데드락

읽기 전

• 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
• 개인적으로 사용해보면서 배운 점을 정리한 글입니다.
• 기술면접만을 준비하기보다 비전공자 입장에서 OS의 기본적인 내용을 짚기 위해 작성되었습니다.

중요도 - 하: 기술 면접에 나올 가능성은 적으나 워낙 기초라 1독은 해야 안심이 될 듯

CPU, 프로세서, 코어

• 프로세서 : 컴퓨터 운용을 위해 명령을 처리하고 반응하기 위한 논리 회로
  • control unit(신호를 보내는 제어장치) + ALU (사칙 연산, 논리 연산)
• CPU : 장치가 해야할 일을 총 지휘하는 프로세서
• 코어 : 각종 연산을 수행하는 CPU의 핵심 요소

CPU 스케쥴링

• CPU 버스트 : 사용자 프로그램의 CPU를 직접 가지고 빠른 명령을 수행하는 과정
  • Add/Store/Load : 레지스터의 두 값을 더함(속도 매우 빠름)/CPU의 계산된 값을 메모리에 저장/메모리의 데이터를 CPU로 읽어들임
• I/O 버스트 : 커널에 의해 입출력 작업을 진행하는 느린 단계의 수행 과정
• I/O 바운드 프로세스 : I/O 버스트가 빈번하여 CPU 버스트가 짧음. 사용자에게 입출력을 받아 처리해가는 대화형 프로그램이 해당됨
• CPU 바운드 프로세스 : 입출력이 드물게 동작하는 계산 위주의 프로세스
• 바운드 프로세스의 스케쥴링 : 일반적으로 I/O 바운드 프로세스가 많다. 따라서 I/O 바운드 프로세스 위주로 먼저 처리하여 I/O 작업을 수행하게 두고 CPU 바운드 프로세스를 처리하면 전체 시스템의 가용률을 높일 수 있다.

CPU 스케쥴러/디스패처

• CPU 스케쥴러 : 준비 큐에서 어떤 프로세스에 CPU를 할당할 지 결정하는 운영체제의 코드다. 그 외 몇 가지 필요한 상황이 있다.
• 비선점형 방식 : 프로세스가 스스로 반납 전까지 CPU를 빼앗지 않음 - FCFS
• 선점형 방식 : CPU로 처리할 작업이 있음에도 강제로 빼앗을 수 있는 방식 - 시분할

1. 실행 상태의 프로세스가 I/O작업을 요청하여 봉쇄상태로 전환
2. 실행 중인 프로세스가 타이머 인터럽트 발생으로 인해 준비상태로 전환
3. I/O 작업 요청했던 프로세스의 I/O 작업 종료로 인터럽트 발생, 준비 상태로 전환
4. CPU에서 실행 상태에 있는 프로세스가 종료

위의 경우 중 1, 4는 스스로 반납하여 비선점형, 2는 선점형 방식이다. 3은 I/O 작업 완료한 프로세스의 우선순위가 높아 CPU를 빼앗을 경우 선점형에 해당한다.

• 디스패처 : 새로 CPU를 할당받은 프로세스가 작업을 수행할 수 있도록 환경설정하는 코드. 문맥교환 동작을 수행한다.
  • 디스패치 지연시간(latency) : 디스패치 동작에 걸리는 시간, 문맥교환 오버헤드에 해당

스케쥴링의 성능 평가

• 시스템 관점 지표 : CPU 이용률과 처리량 등 시스템 가용 정도 관련 지표
  • CPU 이용률 : 전체 시간 중 CPU 가용 시간
  • 처리량 : 주어진 시간 내 준비 상태의 프로세스 중 CPU 버스트를 완료한 프로세스 개수
  • 처리량을 제고하려면 CPU 버스트가 짧은 I/O 바운드 프로세스를 우선 할당하면 된다.
• 사용자 관점 지표 : 소요시간, 대기시간, 응답시간 등 사용자가 체감하는 대기시간 관련 지표
  • 소요시간 : 준비 큐 대기시간 + CPU 사용 시간(I/O 요청으로 자진 반납 시 반납 때까지)
  • 대기시간 : 이번 CPU 버스트가 끝나기까지 준비큐에서 대기한 시간(시분할 시 여러 번 발생 가능)
  • 응답시간 : 첫 번째 CPU 할당받기까지 준비큐에서의 대기시간. 사용자에겐 가장 중요

스케쥴링 알고리즘

• FCFS(First Come First Served) : 준비 큐 진입 순서대로 CPU 할당. 비선점형 방식이다. 먼저 도착한 프로세스에 따라 평균 대기시간이 가변적이다.
  • 콘보이(Convoy) 효과 : 버스트가 긴 프로세스가 먼저 도착해 짧은 프로세스가 오래 대기해야 하는 현상
• 최단 작업 우선(Shortest-Job-First, SJF) : 버스트가 가장 짧은 프로세스에 제일 먼저 CPU를 할당, 평균 대기 시간이 가장 짧다.
  • 비선점형 방식 : 더 짧은 프로세스가 와도 빼앗지 않음
  • 선점형 방식(Shortest Remaining Time First, SRTF) : 더 짧은 프로세스 진입 시 빼앗음
  • 현실적으로 프로세스의 CPU 버스트 시간을 알기 어렵다.(중간에 뺏기 때문)
  • CPU 버스트 예측 : 예측시간 T, 매개변수 α, 실제시간 t에 대해 $T_{n + 1}=\alpha t_n+(1-\alpha)T_n$으로 산출한다. α가 0이면 $T_{n + 1} = T_n$으로 고정값이다. $T_n$을 풀어쓰면 과거의 실제시간으로 치환되어 $(1-\alpha)^j\alpha t_{n-j}$의 꼴로 표현되어 과거로 갈 수록 영향을 줄여나간다.
  • 기아 현상(starvation) : CPU 버스트가 긴 프로세스는 준비 큐에 무한정 대기하게 된다.
  • 전체 시스템 성능 향상을 위해 CPU 버스트가 긴 프로세스를 희생하여 형평성을 간과함
• 우선순위 : 큐에 대기 중인 프로세스에 우선순위를 부여한다. CPU 버스트가 기준이면 SJF가 된다. 각 프로세스마다 중요도는 다를 수밖에 없으므로 기아 현상 발생 여지가 있으며 대기 시간이 길어질수록 순위를 높이는 노화(aging) 기법을 사용하여 해결한다.
• 라운드 로빈(RR) : CPU 할당 시간(time quantum)을 정해 할당한다. 수행시간이 긴 프로세스가 CPU를 점유하더라도 일정 시간 뒤에 CPU 점유를 해제하고 대기열 맨 뒤에 가게 된다.
  • 프로세스의 context를 저장할 수 있기에 가능한 스케쥴링 기법
  • CPU 사용시간이 랜덤한 프로세스가 같이 실행되는 환경에 효과적이다.
  • CPU 버스트 시간에 따라 소요시한이 일정한 비율로 비례하기 때문에 공정하다.
  • 응답시간이 빨라진다. n개의 프로세스에 대해 할당 시간이 q일 경우 최소 $(n - 1)q$시간 내로 첫 할당을 받는다.
• 할당시간이 길면 FCFS가 되고 너무 짧으면 문맥교환 오버헤드가 커진다.
• 멀티레벨 큐 : 준비 큐를 여러 개로 분리해 관리하는 방식.
  • 전위(foreground) 큐 : 대화형 작업을 담는 큐. 빠른 응답 시간을 위해 RR 사용
  • 후위(background) 큐 : 계산 위주 작업을 담는 큐. 응답시간이 중요하지 않아 FCFS 사용
  • 큐에 대한 스케쥴링 : 전위 큐 작업이 모두 끝나면 후위 큐 작업하는 고정 우선순위 방식과(starvation 발생 가능) RR처럼 시간 제약을 일정 비율로 나누는 타임 슬라이스 방식이 있음.
• 멀티레벨 피드백 큐 : 멀티레벨 큐와 유사하나 프로세스가 다른 큐로 이동이 가능함
  • CPU 버스트 짦음 : RR 할당시간이 짧은 상위 큐에서 빨리 처리. 미완료 시 중간 큐 이동
  • CPU 버스트 중간 : RR 할당시간이 긴 중간 큐에서 처리. 미완료 시 하위 큐로 이동
  • CPU 버스트 김 : RR에서 처리가 안될 경우 계산 위주로 간주. FCFS인 하위 큐에서 처리
• 다중처리기 : CPU가 여러 개인 다중처리 시스템에서의 스케쥴링
  • CPU별로 줄세울 때 프로세스의 편중을 막기 위해 부하균형 매커니즘 필요
  • 대칭형 다중처리 : 각 CPU가 알아서 스케쥴링 결정
  • 비대칭형 다중처리 : 한 CPU가 다른 CPU들의 스케쥴을 책임지고 나머지가 한 CPU에 맞춰 움직임
• 실시간 : 주어진 데드라인이 있어 정해진 시간 내로 처리가 중요함
  • 경성(Hard) 실시간 시스템 : 원자로/미사일 등 데드라인이 반드시 지켜져야 함
  • 연성(Soft) 실시간 시스템 : 실시간 스트리밍 등 데드라인이 지켜지지 않더라도 시스템의 붕괴는 발생하지 않음
  • EDF(Early Deadline Fist) : 데드라인에 임박한 요청부터 처리

스케쥴링의 평가

• 큐잉모델 : 이론적 측정 방식, 수학적으로 계산하여 처리량, 평균 대기시간 산출
• 구현 및 실측 : 실제 코드 기반으로 실측값을 기준으로 측정
• 시뮬레이션 : 가상 스케쥴링 프로그램 작성 후 산출

주변 장치 및 입출력 장치 관리 - 인터럽트

• 인터럽트(interrupt) : CPU의 서비스가 필요할 때나 주변 기기가 서비스를 요청할 때 발생시키는 신호이다. CPU는 인터럽트를 받으면 작업 상태를 저장해두고 인터럽트를 처리한다.
• 인터럽트 처리 루틴(interrupt service routine) / 인터럽트 핸들러 (interrupt handler) : 인터럽트는 장치 종류나 상황에 따라 종류가 다양하므로 그에 따라 해야 할 작업을 정의한 프로그램 코드이다. 커널에 존재하는 CPU 스케쥴링, 메모리 관리 루틴과 마찬가지로 커널코드의 일부이다.
• 인터럽트 핸들링 : 인터럽트가 발생한 경우 처리해야할 일들의 절차, 인터럽트 처리 루틴 / 인터럽트 핸들러에 정의된 내용을 말한다.
  • A 프로그램이 실행 중 인터럽트가 발생하면 A의 현재 상태(CPU에서 실행 중인 명령의 메모리 주소 등)를 저장해야 한다. 프로그램 실행 시 CPU의 임시 기억장치인 레지스터에 읽기 / 쓰기 작업을 하는데 인터럽트로 인해 새로운 명령이 실행되면 기존 레지스터를 비워버리기 때문에 이러한 상태를 저장한 뒤에야 인터럽트 처리를 시작한다.
• 프로세스 제어 블록(process control block, PCB) : OS가 현재 시스템 내에서 실행되는 프로그램들을 관리하기 위해 사용하는 자료구조이다. 프로그램마다 하나씩 존재하며 프로그램이 실행 중인 코드의 메모리 주소, 레지스터 값, 하드웨어 상태등을 저장하여 프로그램의 어느 부분이 실행 중이였는 지 알 수 있다.
  • 프로그램이 실행되는 중 인터럽트가 발생하면 PCB에 저장 후 CPU의 제어권이 인터럽트 처리 루틴으로 넘어간다. 인터럽트 처리가 끝나면 PCB에서 상태를 CPU에 복원해 인터럽트되기 직전의 상태에서 실행을 이어간다.
• 컨트롤러 : CPU에 인터럽트를 송신하기 위한 주변기기의 작은 CPU
• 로컬 버퍼(local buffer) : 메모리에 데이터를 보내기 전 작업을 완료할 때까지 저장하는 공간
• 인터럽트 라인(interrupt line) : 인터럽트 수신 시 CPU에 신호를 전달하는 장치
• 인터럽트 벡터(interrupt vector) : 인터럽트 종류마다 번호를 정해서 그에 맞는 인터럽트 처리 루틴과 매칭시키는 자료 구조
• 소프트웨어 인터럽트(software interrupt) : 하드웨어로부터가 아니라 소프트웨어로부터 발생된 인터럽트이다. 주로, 트랩(trap)이라 불러서 구분한다. 예외 상황(Exception)과 시스템 콜(System Call)이 있다.
  • 예외 상황(Exception) : 사용자 프로그램이 0으로 나누는 시도를 하거나 자신의 할당 메모리 바깥에 접근하는 등 권한 없는 작업 시도에 대한 처리를 발생시키는 인터럽트이다.
  • 시스템 콜 : 사용자 프로그램이 운영체제 내부에 정의된 코드를 실행하고 싶을 때 OS에 전달하는 서비스 요청이다.
    • 프로그램 동작 중 키보드 입력 / 화면 출력 등이 필요할 때 이미 커널에 적재된 코드를 요청한다.

입출력 관리

• 동기식 입출력(Synchronous I/O) : 어떤 프로그램이 입출력 요청을 했을 때 입출력 작업을 완료해야 그 후속작업을 진행하는 방식
  • 예시 :
    1. A 프로그램이 디스크를 읽는 트랩을 발생시킨다.
    2. 입출력 작업이 끝날 때까지 A 프로세스를 봉쇄 상태(blocked state)로 전환시켜 입출력 작업 완료 전까지 CPU를 할당하지 않는다.
    3. 그 동안 다음 대기열의 B 프로그램에 할당하여 작업을 계속 진행한다.
    4. 이후 A 프로세스가 호출한 디스크 입출력 과정이 끝나 CPU에 인터럽트가 수신되면 A 프로그램의 봉쇄 상태를 해제하여 CPU 대기열 큐에 적재한다.
    5. 자신의 차례가 되면 입출력 이후의 작업을 진행한다.동기성 보장 : 입출력 트랩을 발생시킨 A가 봉쇄 상태로 전환되고 다음에 CPU를 할당받은 B 프로그램 또한 동일한 곳에 접근하고자 입출력 트랩을 발생시킨 경우 입출력 장치가 A에서 B가 아닌 B에서 A 순서대로 처리하여 발생하는 문제를 방지하고자 장치 별로 큐를 두고 요청한 순서대로 처리하게끔 보장한다.
• 비동기식 입출력(Asynchronous I/O) : 입출력 작업이 끝날 때까지 기다리지 않고 입출력 작업으로 가져온 데이터가 필요한 경우는 입출력이 끝나고 수행하되 굳이 필요없는 작업은 그대로 이어서 진행한다. 이를테면, 디스크 쓰기는 쓰기 명령을 내린 뒤에 다음 작업을 처리해도 되므로 비동기식 입출력을 사용할 수 있다. 물론 비동기식 입출력의 경우에도 입출력 작업이 끝난 뒤에도 CPU로 작업이 완료되었다는 인터럽트를 전송한다.

• DMA(Direct Memory Access) : 원칙적으로 메모리는 CPU만 접근할 수 있어 CPU를 제외한 장치가 메모리 데이터에 접근하기 위해서는 CPU에 인터럽트를 발생시켜 CPU가 대행해야만 한다. 그러나 매번 CPU가 대행할 경우 기존 업무를 방해받을 수 있어 중간에 CPU말고도 접근이 가능한 장치인 DMA를 둬서 입출력 장치의 메모리 접근 요청에 의한 CPU로의 인터럽트 빈도를 줄여준다.
• 즉, 로컬 버퍼에서 메모리로 데이터를 읽는 작업은 DMA가 수행하며 단위는 byte가 아니라 block 단위로 크게 읽어온다.

보안

• 하드웨어 관점 : 커널 모드와 사용자 모드를 분리하여 실행할 수 있는 명령을 구분한다. 그리고 CPU는 모드 비트 0과 1을 둬서 0인 경우에만 커널 모드의 명령을 수행한다. 1은 사용자 프로그램이 CPU를 점유했을 때 마킹된다. 따라서, 프로그램이 시스템 콜을 하면 운영체제가 CPU를 점유하여 자동으로 모드 비트가 0으로 마킹되고 작업이 완료되면 사용자 프로그램에 CPU를 넘기면서 모드 비트를 1로 세팅한다.
• 메모리 관점 : 하나의 프로그램이 한 영역의 메모리에 적재될 경우 기준 레지스터와 한계 레지스터를 두어 참조값이 범위 내에 있는 지 확인한다. 벗어난 경우 예외상황이라는 트랩을 발생시켜서 종료시킨다.
• CPU 관점 : 타이머라는 장치를 둬서 CPU를 무한 점유하는 일이 없도록 한다. 시분할 시스템에도 사용된다.

디스크 관리

• 논리 블럭 : 데이터가 저장되는 단위
• 섹터 : 논리 블럭이 저장되는 디스크 내 물리적 위치
• 트랙 : 중심에서 거리가 같은 섹터 집합 (2차원 배열에서의 1개의 row와 유사 원판의 회전은 col을 옮긴다고 간주)
• 실린더 : 여러 개의 원판에서 중심으로부터 거리가 같은 트랙의 집합 (2차원 배열의 row와 유사)

디스크 스케쥴링

• 탐색시간 : 헤드를 데이터가 위치한 실린더까지 옮기는 시간
• 회전지연시간 : 디스크의 섹터가 헤드 위치로 도달하기까지의 시간
• 전송시간 : 섹터에서 데이터를 읽고 쓰는 시간
• 회전지연 시간과 전송 시간은 물리적 시간으로 OS는 탐색 시간을 통제하려 노력
• FCFS 스케쥴링 : 요청 순서대로 헤드를 이동
• SSTF(Shortest Seek Time First) : 헤드의 현재 위치에서 가장 가까운 요청부터 이동
  • starvation 문제 발생 가능
• SCAN : 헤드를 양 끝단으로 이동시키며 그 경로에 있는 요청 처리
  • 엘리베이터 스케쥴링 알고리즘이라고도 함
  • C-SCAN(Circular-SCAN) : 양 끝을 왕복하며 탐색하는 SCAN 알고리즘은 양 끝단의 경우 탐색 시간이 지연되기에 한쪽 끝으로 도달하면 방향을 바꾼 뒤엔 요청을 처리하지 않고 다시 출발점으로 회귀
• LOOK : SCAN 알고리즘의 개량 버전. 헤드가 이동하는 방향에 더 이상 요청이 없으면 방향 전환
  • C-LOOK : C-SCAN이 출발점으로 회귀하는 것과 달리 번호가 가장 낮은 요청으로 이동하여 처리 시작

다중디스크 스케쥴링

• 일부 디스크의 오류에도 지속적인 서비스가 가능하며 정보의 유실 방지 가능
• 작업을 수행할 디스크의 결정문제까지 포함, 디스크들의 부하 균형(load balancing) 고려해야 함.

관련 포스팅

1.기술면접을 위한 OS 개념정리 02 - 프로세스, 스레드

2.기술면접을 위한 OS 개념정리 03 - 메모리, 가상 메모리 관리, 웹캐싱 기법

3.기술면접을 위한 OS 개념정리 04 - 프로세스 동기화, 데드락

읽기 전

• 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
• 개인적으로 배운 점을 정리한 글입니다.

문제 링크

BOJ #9345 디지털 비디오 디스크(DVDs)

문제 풀이

세그먼트 트리 비재귀 구현 포스팅을 작성하게 만든 문제다. Python은 어림도 없고 pypy3에서도 비재귀 방식으로 세그먼트 트리를 작성해야 했다. 풀이에는 최대-최소 알고리즘을 썼는데 생각해보니 그냥 최대 세그먼트 트리와 최소 세그먼트 트리를 분리해 구현하는게 메모리 측면에서는 손해겠지만 시간 측면에서는 손해가 아닐 수도 있겠다는 생각이 들었다.

기본 원리는 선반에 DVD가 좌표값대로 들어있음에 착안하여 left부터 right까지의 DVD를 선택했을 때 left부터 right까지의 DVD가 존재해야 하므로 최솟값이 left이고 최댓값이 right이면 해당 범위의 DVD가 모두 존재함을 보장할 수 있겠다.

• 비재귀 방식으로 0 ~ N -1 배열에 대한 세그먼트 트리 생성
• 교체 시 교체된 ㄱ밧으로 최댓/최솟값 업데이트
• 조회 시 최솟값에 left, 최댓값에 right가 매칭되면"YES" 출력, 그렇지 않으면 "NO" 출력

python 코드

import sys
input = sys.stdin.readline

def solve():
    def max_init():
        for i in range(N - 1, 0, -1):
            tree[i] = max(tree[i << 1], tree[i << 1 | 1])

    def min_init():
        for i in range(N - 1, 0, -1):
            tree[i] = min(tree[i << 1], tree[i < 1 | 1])

    def max_query(l, r):
        sol = 0
        l += N
        r += N
        while l < r:
            if l % 2 == 1:
                sol = max(tree[l], sol)
                l += 1
            if r % 2 == 1:
                sol = max(tree[r - 1], sol)
            l //= 2
            r //= 2
        return sol

    def min_query(l, r):
        sol = 0
        l += N
        r += N
        while l < r:
            if l % 2 == 1:
                sol = min(tree[l], sol)
                l += 1
            if r % 2 == 1:
                sol = min(tree[r - 1], sol)
                r -= 1
            l //= 2
            r //= 2
        return sol

    def max_update(i, val):
        tree[N + i] = val
        i += N
        while i > 1:
            tree[i >> 1] = max(tree[i], tree[i ^ 1])

    def min_update(i, val):
        tree[N + i] = val
        i += N
        while i > 1:
            tree[i >> 1] = min(tree[i], tree[i ^ 1])

    for _ in range(int(input())):
        N, K = map(int, input().split())
        INF = float('inf')
        min_tree = [INF] * (2 * N)
        max_tree = [-INF] * (2 * N)
        nums = [0] * N
        for i in range(N):
            max_tree[N + i] = i
            min_tree[N + i] = i
            nums = [i]
        for _ in range(K):
            q, a, b = map(int, input().split())
            if q:
                min_v = min_query(a, b + 1)
                max_v = max_query(a, b + 1)
                if min_v == a and max_v == b:
                    print("YES")
                else:
                    print("NO")
            else:
                nums[a], nums[b] = nums[b], nums[a]
                max_update(a, nums[a])
                min_update(a, nums[a])
                max_update(b, nums[b])
                min_update(b, nums[b])
solve()

읽기 전

• 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
• 개인적으로 사용해보면서 배운 점을 정리한 글입니다.

세그먼트 트리의 비재귀적(반복문) 구현

백준 문제를 풀다가 세그먼트 트리로 푸는 문제인데 시간 제약이 빠듯한 문제를 만났다. 도저히 통과가 안되길래 질문글을 봤더니 pypy3로 제출해야 함은 물론이거니와 그마저도 재귀는 시간이 오래 걸려 비재귀 방식으로 구현해야 한단다. 찾아본 결과 python으로 세그먼트 트리를 비재귀적 방식을 사용해 정리한 포스팅을 찾을 수 없어 개인적으로 정리하게 되었다. 구현 방식은 비교적 간단한 편이다. 재귀로 구현한 포스팅은 세그먼트 트리(Segment Tree)에 정리한 바 있다.

재귀 vs 비재귀(반복) - Recursion VS Loop

세그먼트 트리의 재귀적 구현 방식의 핵심은 분할 정복이었다. 따라서 리프 노드의 위치가 모여있지 않고 떨어진 경우가 있는 반면 비재귀적인 방식은 먼저 정해진 위치에 기존 배열 원소를 리프 노드로 두고 힙을 역으로 구성하듯이 접근한다. 배열 nums = [1, 3, 5, 2, 6, 4]를 예를 들어 구현해보자.

세그먼트 트리 생성

먼저 주어진 배열 길이 N에 대해 각 배열 원소의 좌표를 더한 위치에 값을 저장한다. 그리고 트리에서의 양쪽 자식노드는 [i * 2], [i * 2 + 1]이므로 해당 위치의 값을 더해 N - 1부터 1좌표까지 역으로 완성해나간다. 그러면 1좌표에 배열의 모든 원소 합이 들어가게 된다. Python코드로 구현해보자.

Python 코드

def init(tree, N):
    for i in range(N - 1, 0, -1):
        tree[i] = tree[i << 1] + tree[i << 1 | 1]

nums = [1, 3, 5, 2, 6, 4]
print(f'nums: {nums}')
segment_tree = [0] * (2 * len(nums))
N = len(nums)
for i in range(len(nums)):
    segment_tree[N + i] = nums[i]
init(segment_tree, N)
print(f'segment tree : {segment_tree}')

<<는 우측으로 1비트 옮김을 의미하고 현재 값에 2를 곱하는 연산과 결과가 동일하다. |는 or 연산으로 <<연산 후 0이 된 1의 자리에 or연산을 적용하면 1을 더한 값과 동일해진다. tree[i] = tree[i * 2] + tree[i * 2 + 1]로 바꿔도 동작 결과는 동일하다.

세그먼트 트리 쿼리

반복문을 사용한 세그먼트 트리의 쿼리 범위는 좌/우측 좌표가 주어졌을 때 [left, right)이다. right좌표를 포함하지 않기 때문에 right좌표까지 포함한 값을 구하고 싶다면 right + 1을 주어야 하고 우측 좌표가 배열 길이 N보다 크다면 N으로 바꿔 조회 시 오류가 없게끔 한다. 1좌표부터 3좌표까지의 합을 구한다고 가정하면 함수에 left = 1, right = 4를 입력해야 한다. Python 코드로 구현해보자.

Python 코드

def query(tree, N, left, right):
    result = 0
    left += N
    right += N
    while left < right:
        if left % 2 == 1:
            result += tree[left]
            left += 1
        if right % 2 == 1:
            result += tree[right - 1]
            right -= 1
        left //= 2
        right //= 2
    return result

print(f'idx 1 to 3 : {nums[1:4]}')
print(f'sum 1 to 3 : {query(segment_tree, N, 1, 4)}')

위 그림이 쿼리 반복문의 첫 시작이다. left 좌표에 N을 더한 결과가 7이고 left % 2 == 1이므로 해당 좌표의 값 3을 더하고 left에 1을 더하여 2를 나누면 4가 된다. right 좌표에 N을 더한 결과가 10이므로 그대로 2를 나눠 5가 된다.

left가 4가 되었고 left % 2 == 0이 되어 그대로 2로 나눈 값 2가 된다. right는 5가 되었고 right % 2 == 1이므로 tree[right - 1]의 값 7을 더하고 right 좌표에 1을 빼고 2로 나누면 2가 된다. 다음 반복은 left < right가 성립하므로 진행되지 않는다. 쿼리 결과가 10인데 이는 1좌표에서 3좌표까지의 합 3 + 5 + 2와 동일하다.

세그먼트 트리 갱신

기존 배열의 특정 좌표의 값을 수정하고자 한다면 세그먼트 트리의 값도 수정해야 한다. 트리를 생성하는 과정과 유사하다. 기존 배열의 원소와 대응되는 트리 노드의 좌표를 알고 있으므로(N + i) 먼저 리프노드의 값을 반영하고 그 값을 기준으로 루트 노드에 다다를 때까지 반복한다.

자식 노드부터 출발했으므로 부모 노드의 값을 변경해야 한다. 부모 노드는 현재 좌표 idx 기준 우측으로 1비트 옮겨 2로 나눈 값과 동일하다. 그렇다면 현재 좌표와 부모 노드의 좌표는 구했으나 부모 노드의 다른 자식 노드의 좌표값을 구해야 한다. 산술적으로 현재 좌표가 2의 배수면 1을 더한 값이고 2의 배수가 아니라면 1을 뺀 값이다. 이를 간단하게 표현하면 1과 xor 연산한 값이라 말할 수 있겠다.

python 코드

def update(tree, N, i, val):
    tree[N +i] = val
    i += N
    while i > 1:
        tree[i >> 1] = tree[i] + tree[i ^ 1]
        i >>= 1

update(segment_tree, N, 1, 4)
nums[1] = 4
print(f'idx 1 to 3 : {nums[1:4]}')
print(f'sum 1 to 3 : {query(segment_tree, N, 1, 4)}')

전체 코드

from math import ceil, log


def init(tree, N):
    for i in range(N - 1, 0, -1):
        tree[i] = tree[i << 1] + tree[i << 1 | 1]


def query(tree, N, left, right):
    result = 0
    left += N
    right += N
    while left < right:
        if left % 2 == 1:
            result += tree[left]
            left += 1
        if right % 2 == 1:
            result += tree[right - 1]
            right -= 1
        left //= 2
        right //= 2
    return result


def update(tree, N, i, val):
    tree[N + i] = val
    i += N
    while i > 1:
        tree[i >> 1] = tree[i] + tree[i ^ 1]
        i >>= 1


nums = [1, 3, 5, 2, 6, 4]
print(f'nums: {nums}')
segment_tree = [0] * (2 * len(nums))
N = len(nums)
for i in range(len(nums)):
    segment_tree[N + i] = nums[i]
init(segment_tree, N)
print(f'segment tree : {segment_tree}')

print(f'idx 1 to 3 : {nums[1:4]}')
print(f'sum 1 to 3 : {query(segment_tree, N, 1, 4)}')

update(segment_tree, N, 1, 4)
nums[1] = 4
print(f'idx 1 to 3 : {nums[1:4]}')
print(f'sum 1 to 3 : {query(segment_tree, N, 1, 4)}')