읽기 전
- 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
- 개인적으로 배운 점을 정리한 글입니다.
- 개념이 섞인 채 정리된 포스팅이 많아서(심지어 긱스도 가독성이 영...) 최대한 여러 군데에서 정보를 모아 정리했습니다.
B-Tree란?
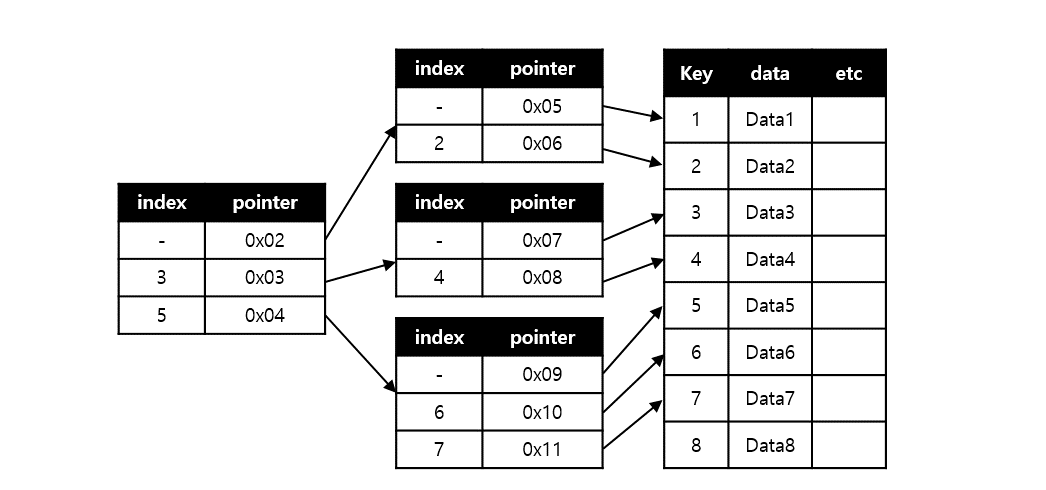
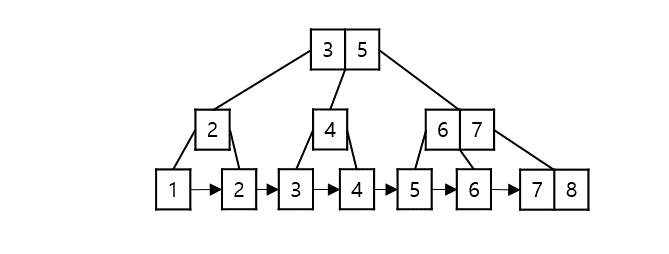
자가 균형 트리로 AVL 트리, 레드-블랙 트리와 더불어 skewed tree를 해결할 수 있는 자료구조 중 하나다. 다만, AVL 트리나 레드-블랙 트리를 모든 데이터가 메모리에 적재할 수 있는 경우에 적용함과는 달리 B-Tree는 대용량 데이터를 다뤄야하는 DB나 디스크에 주로 적용된다.
대부분 트리에서의 연산이 높이에 따라 결정됨을 볼 때 B-Tree는 h를 줄이기 위해 B-Tree의 노드에 가능한 많은 값을 집어넣어 높이를 낮춤으로써 fat tree의 형태를 보인다.
일반적으로 B-Tree 노드의 크기는 디스크 블록의 크기에 따라 결정되며 높이를 낮춤으로써 디스크로의 접근지연 시간을 최소화한다.
B-Tree의 시간복잡도

B-Tree의 성질
노드 내 자료를 key, 자식은 child로 정의한다. 각 노드는 자신이 리프 노드인지 표시하기 위한 bool값을 갖는다.
모든 리프 노드는 같은 레벨에 있어야 한다.
노드 내 자료는 모두 오름차순 정렬된 상태다.
- 노드 내 키 값 $k_1$과 $k_2$ 사이의 child의 모든 키는 $k_1$과 $k_2$ 사이에 속한다.
최소차수 $t$(Minimum Degree)에 대해 노드는 최소 $t - 1$개의 key를 가져야 하고 최대 $2t-1$개의 key를 가질 수 있다.
- 삽입해야 하는 노드의 key 개수가 $2t-1$개라면 노드를 쪼개는 split 과정을 수행
B-Tree의 계수 $M$(order)은 노드가 가질 수 있는 자식 노드의 최대 개수를 의미한다. 일반적으로 M차 B-Tree에서의 M이 계수를 지칭한다.
루트 노드가 리프 노드가 아니라면 루트는 적어도 2개의 자식 노드와 1개의 키를 갖는다.
노드가 k개의 key를 가지면 child의 수는 k + 1개이다.
여러 정리된 글에서 degree와 order의 관계에 대해 명시하지 않고 섞어서 서술하고 있다. 적어도 2 * minimum degree($t$) - 1 = maximum degree = order - 1 정도로 인지하고 만약 order가 홀수라면 minimum degree $=t=\lfloor\cfrac{M}{2}\rfloor$이다.
B-Tree에서의 검색(Search)
BST와 비슷하나 key의 개수가 여러 개이고 그에 따라 적절히 child를 선정하는 로직을 추가해야 한다. 현재 노드에 값이 존재하는지 여부는 키들이 정렬되어 있으므로 이분탐색으로 빠르게 찾을 수 있다. 노드에 값이 없다면 찾고자 하는 값보다 큰 값 중 최솟값(lower bound)의 좌표대로 자식 노드를 순회한다. 만약 탐색 노드가 리프 노드에도 없다면 트리에 값이 존재하지 않음을 의미한다.
class BTreeNode:
def __init__(self, keys, children, is_leaf):
self.keys = keys
self.children = children
self.is_leaf = is_leaf
class BTree:
def __init__(self, t):
self.root = BTreeNode([], [], True)
self.t = t
def search(self, key):
return self._search_key(key, self.root)
def _search_key(self, key, node):
# get binary search lower bound index
# if current node has key, return
# if key dosen't exist and cur node is leaf node, return False
# if cur node isn't leaf node, call recursive func for child[lower_bound]
i = bisect.bisect_left(node.keys, key)
if i < len(node.keys) and key == node.keys[i]:
return (node, i)
elif node.is_leaf:
return None
else:
return self._search_key(key, node.children[i])
B-Tree에서의 삽입(Insert)
- 루트 노드가 full상태인지 체크한다.
- full이면 중앙값을 기준으로 새로운 루트 노드 생성한 뒤 양 옆을 새로운 루트 노드의 child로 생성(split)
- 루트 노드가 full이 아니라면 삽입과정을 수행한다.
- 이진 탐색으로 lower bound 좌표 산출, linear 탐색으로도 가능
- 만약 현재 노드가 리프 노드면 해당 좌표에 삽입
- 리프 노드가 아니라면 현재 노드가 full 상태인지 체크하여 split 수행
- 재귀 호출로 lower bound 좌표를 갖는 자식 노드에 대해 수행
def insert(self, key):
# if root node is full, make root node as child
# split new root as child
# new root would get value(median) from old root
# call insert routine from root to leaf node recursively
if len(self.root.keys) == 2 * self.t - 1: # root is full
self.root = BTreeNode([], [self.root], False)
self._split_child(self.root, 0)
self._insert_key(key, self.root)
def _insert_key(self, key, node):
# get lower bound idx -> keys[i] > key
# if current node is leaf, then insert key at idx
# else, check ith child is full. if is, do split ith child
# after split ith child, add ith child's median value in cur node key
# check value and change lower bound idx for key
# call insert routine to ith child
i = bisect.bisect_left(node.keys, key)
if node.is_leaf:
node.keys.insert(i, key)
else:
if len(node.children[i].keys) == 2 * self.t - 1:
self._split_child(node, i)
if key > node.keys[i]:
i = i + 1
self._insert_key(key, node.children[i])
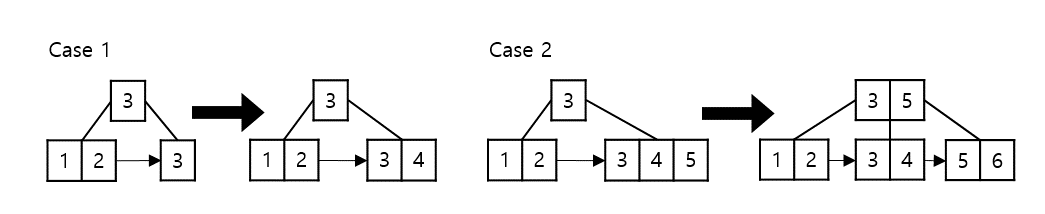
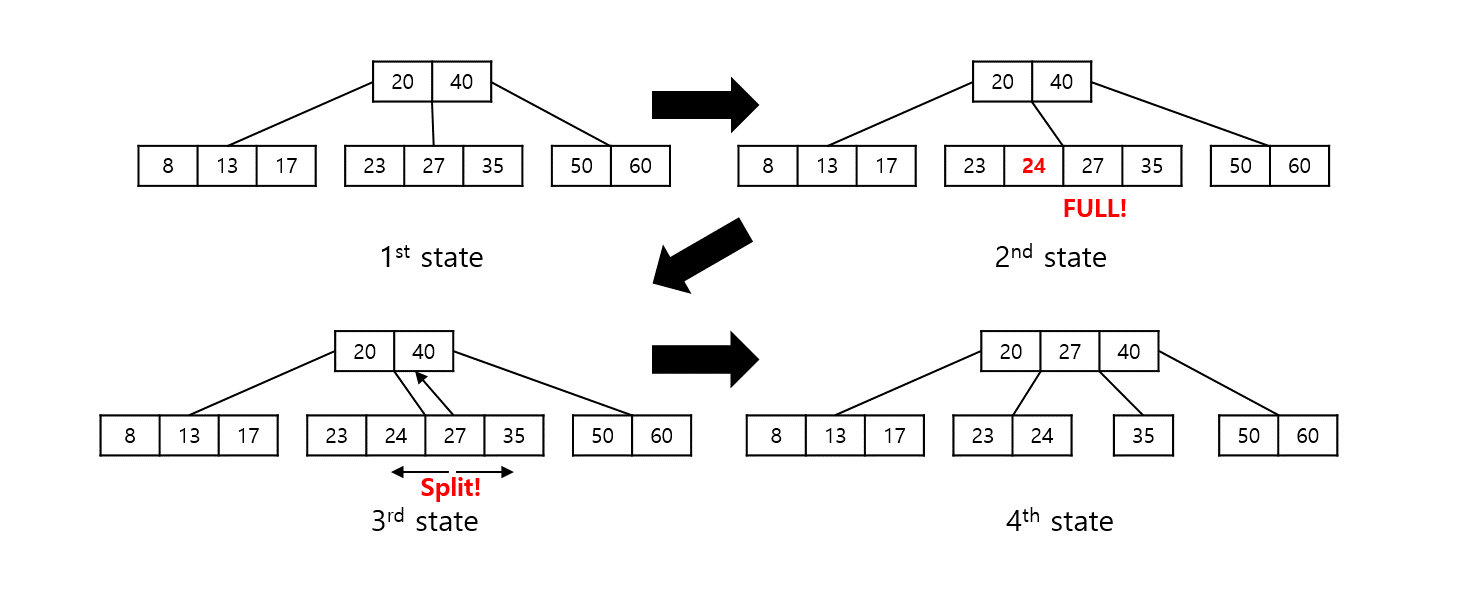
split 과정
중간값을 기준으로 주어진 좌표의 자식 노드를 양쪽으로 쪼개고 중간값을 위쪽 노드로 올리는 작업이다.
def _split_child(self, node, i):
# get ith child from node
# split key and child half, except median value
# get median value and insert in node
# change ith child to left part(cause smaller then median)
# insert left in i + 1 idx (case bigger than median)
c = node.children[i]
c_l = BTreeNode(c.keys[0:self.t - 1], c.children[0:self.t], c.is_leaf)
c_r = BTreeNode(c.keys[self.t:2 * self.t - 1],
c.children[self.t:2 * self.t], c.is_leaf)
median = c.keys[self.t - 1]
node.keys.insert(i, median)
node.children[i] = c_l
node.children.insert(i + 1, c_r)
B-Tree에서의 삭제(Delete)
여느 탐색 트리와 마찬가지로 삭제 과정이 꽤 어렵다. 데이터를 삭제한 뒤 루트 노드를 제외한 모든 노드는 minimum degree만큼의 key를 가져야 하는 조건에 위배될 수 있기 때문에 reconstruct하는 과정이 필요하다. 으레 그렇듯이 이 과정이 난이도 상승을 초래한다.
주의점 : 작업 노드가 키 삭제 후에도 $\lfloor\cfrac{M}{2}\rfloor=t-1$만큼의 key를 가지게끔 보장해야 한다.
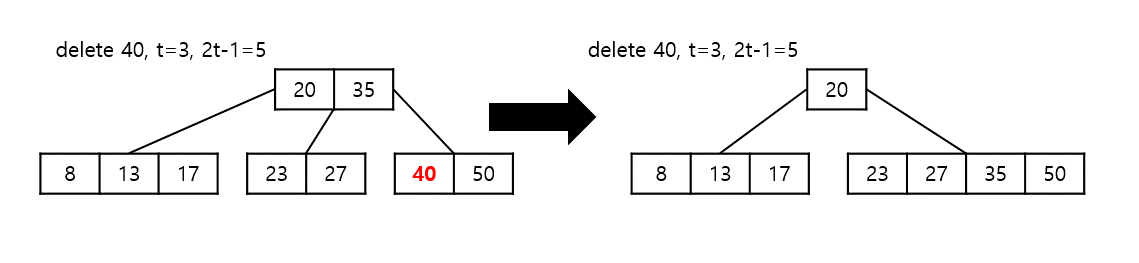
리프 노드에서 key를 삭제하는 경우
a) 현재 key의 개수가 $t-1$보다 큰 경우 : 그대로 삭제 후 종료
b) 현재 key의 개수가 $t-1$인 경우
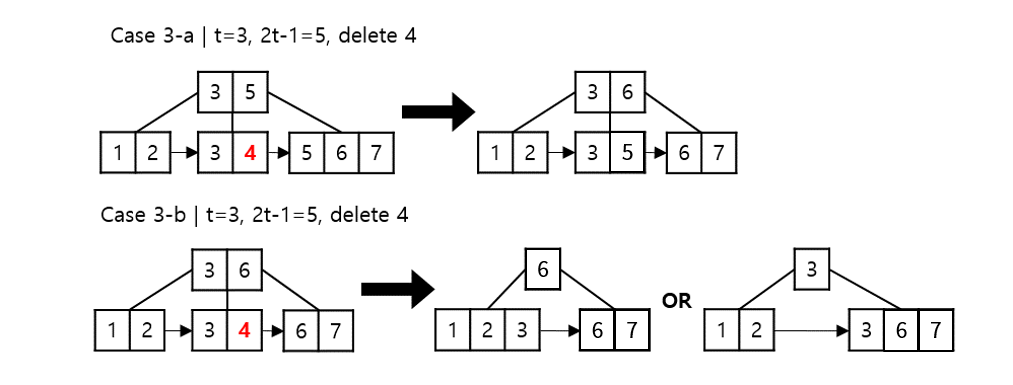
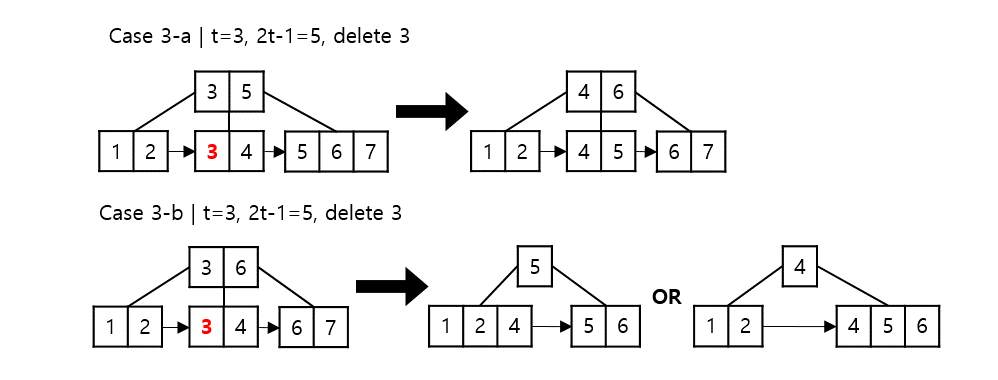
내부 노드에서 key를 삭제하는 경우 - 노드나 자식 중 하나의 key 개수가 $t -1$보다 큰 경우
데이터의 삭제는 리프 노드에서 작업하는 게 편리하므로 대체해 줄 데이터를 찾아야 한다. 일반적으로 inorder predecessor(key보다 작은 값 중 최댓값)이나 inorder successor(key보다 큰 값 중 최솟값)을 대체하게 된다. 이는 BST, 레드-블랙 트리 등에서의 삭제 key를 대체하는 방법과 유사하다. 포스팅에서는 successor를 사용한다.
- inorder successor key를 찾아서 현재 노드의 삭제하고자 하는 key와 교체한다.
- 이후 값을 교체한 지점(반드시 리프 노드임)으로 가서 1번 처리루틴으로 회귀한다.
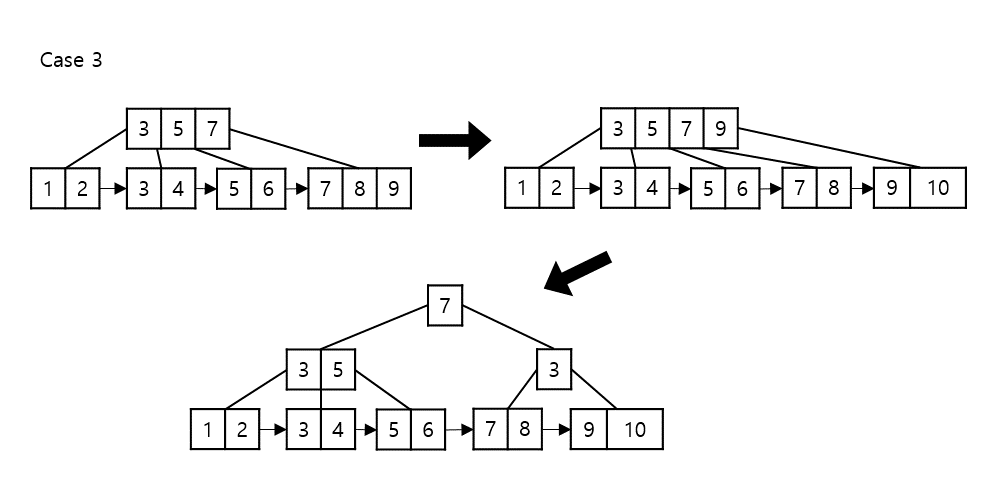
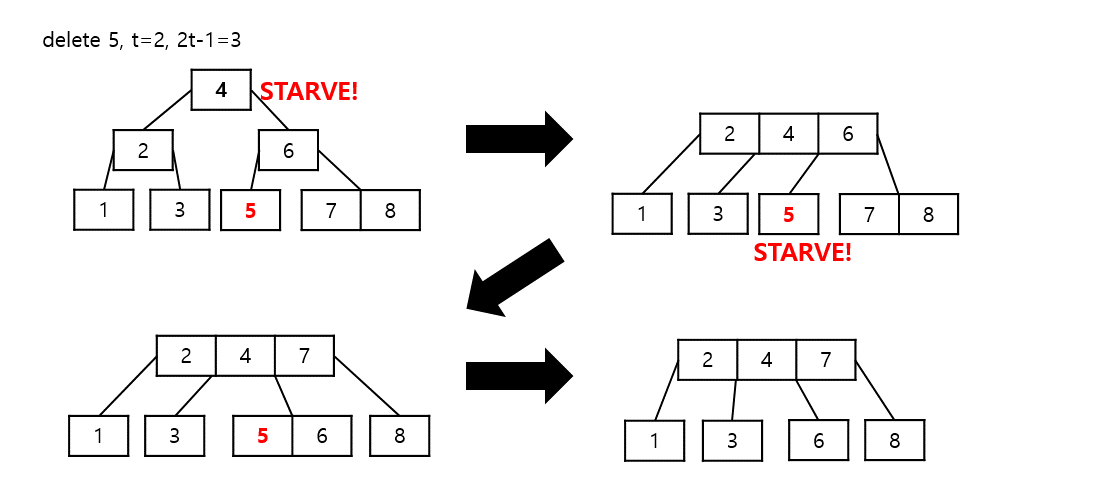
내부 노드에서 key를 삭제하는 경우 - 노드나 자식 모두 key 개수가 $t -1$인경우
a) 노드의 삭제할 key를 삭제하고 key 사이의 양쪽 노드를 하나로 병합한다.
b) 삭제된 key의 부모 key를 형제 노드에 붙인 뒤 3-a에서 병합한 노드를 옮겨진 key의 자식 노드로 설정한다.
- 부모 key가 더해진 인접한 형제 노드 key 개수가 $2t-1$보다 크다면 삽입 연산의 split 과정을 수행

B-Tree에서의 삭제 구현
B-Tree 삭제 방법에 관해선 위 내용이 주를 이룬다. 다만, 구현하면서 다소 번잡한 점이 있기에 하향식 접근을 채택한 방법도 소개하고자 한다.
삭제 연산을 위해 노드에 접근하면서 다음 행선지 노드가 결정되면 해당 노드의 key 개수가 $t-1$개인지 체크 후 $t-1$이라면 reconstruct를 수행, key 개수를 늘려준다.
삭제 연산을 위해 진행하는 모든 경로에 대해 빈곤한 상태(key의 개수가 $t-1$개)라면 재조정하면서 탐색하는 방식이다. 구현, 이해에는 굉장히 편리하나 보조연산의 횟수가 늘어나 성능에는 유리한 점이 없다. 삭제 연산 시 다음 행선지 노드의 key 개수가 $t-1$보다 크다는 점을 보장한다면 삭제연산이 보다 수월해질 것이다. 이 방법은 "Introduction To Algorithms" 책에 소개된 방법이라는 듯하다.
root 노드의 key가 1개이고 양쪽 자식 노드의 key 개수가 $t - 1$개일 때
- 높이가 줄어드는 작업이 필요하다.
- 새로운 루트 노드를 선언, 키는 왼쪽 자식, 기존 root, 오른쪽 자식의 키를 넣고 자식 노드는 왼족, 오른쪽 자식의 자식노드를 넣는다.
- 새로운 루트 노드의 자식 노드가 없다면 높이가 1이므로 leaf 태크를 True로 바꾼다.
1번을 통과하여 삭제 루틴 진행 시, 이진 탐색 lower bound 좌표 산출, 현재 노드에 존재하는지 체크
a) 현재 노드에 존재하고 리프 노드인 경우
- 앞서 $t-1$보다 크게끔 로직이 보장해주므로 그대로 pop
b) 내부 노드일 경우 inorder successor 값을 찾아서 교체한다.
- inorder successor 자리에 있는 값을 삭제해야 하므로 행선지는 1좌표를 더해야 한다.
- 위치가 바뀌었으므로 다음 행선지를 i+1 좌표 자식 노드로 진행한다.
매칭되지 않은 경우 다음 행선지 진입에 앞서 다음 노드가 $t-1$개의 key를 갖는지 체크, $t-1$개라면 reconstruct 진행
a) 왼쪽, 오른쪽 형제 노드 중 하나사 $t-1$개보다 key가 많은 경우
- 부모의 key를 현재 노드에 삽입하고 $t-1$보다 큰 노드에서 key를 부모로 이동
b) 양쪽 모두 $t-1$개인 경우
- 부모 key와 형제 노드, 현재 노드를 하나로 병합
- 부모는 $t-1$보다 크다는 것을 앞 단계에서 보장받음
- 현재 노드 + 부모 키 + 현재 노드 = $2t-1$로 full상태가 됨
3번 과정 수행한 뒤 새롭게 lower bound 좌표 선정하여 진행
def delete(self, key):
# if root key cnt is 1 and all child's node key count also t - 1
# B-Tree would shrink to h - 1
# so, before delete operation, root needs to be preprocessed
if len(self.root.keys) == 1:
root = self.root
t = self.t
left, right = root.children[0], root.children[1]
if len(left.keys) == t - 1 and len(right.keys) == t - 1:
self.root = BTreeNode([], [], False)
self.root.keys.extend(left.keys)
self.root.keys.extend(root.keys)
self.root.keys.extend(right.keys)
self.root.children.extend(left.children)
self.root.children.extend(right.children)
if len(self.root.children) == 0:
self.root.is_leaf = True
self._delete_key(key, self.root)
def _delete_key(self, key, node):
i = bisect.bisect_left(node.keys, key)
# if key matched from currnet node
if i < len(node.keys) and node.keys[i] == key:
if node.is_leaf:
node.keys.pop(i)
return
else:
successor = self._find_successor(node.children[i + 1])
node.keys[i], successor.keys[0] = successor.keys[0], node.keys[i]
self._delete_key(key, node.children[i + 1])
# if key didn't matched then check next node status
else:
if len(node.children[i].keys) == self.t - 1:
self._delete_balancing(node.children[i], node, i)
i = bisect.bisect_left(node.keys, key)
self._delete_key(key, node.children[i])
def _delete_balancing(self, node, parent, i):
# if next destination index is last pos
# next dst just has left siblings
if i == len(parent.children) - 1:
if len(parent.children[i - 1].keys) > self.t - 1:
node.keys.insert(0, parent.keys.pop())
parent.keys.append(parent.children[i - 1].keys.pop())
if len(parent.children[i - 1].children) > 0:
node.children.insert(
0, parent.children[i - 1].children.pop())
else:
parent.children[i - 1].keys.append(parent.keys.pop())
parent.children[i - 1].keys.extend(node.keys)
parent.children.pop()
# if next destination index is first pos
# next dst just has right siblings
elif i == 0:
if len(parent.children[i + 1].keys) > self.t - 1:
node.keys.append(parent.keys.pop(0))
parent.keys.insert(0, parent.children[i + 1].keys.pop(0))
if len(parent.children[i + 1].children) > 0:
node.children.append(
parent.children[i + 1].children.pop(0))
else:
parent.children[i + 1].keys.insert(0, parent.keys.pop(0))
for k in node.keys:
parent.children[i + 1].keys.insert(0, k)
parent.children.pop(0)
else:
if len(parent.children[i - 1].keys) > self.t - 1:
node.keys.insert(0, parent.keys[i])
parent.keys[i] = parent.children[i - 1].keys.pop()
if len(parent.children[i - 1].children) > 0:
node.children.insert(
0, parent.children[i - 1].children.pop())
elif len(parent.children[i + 1].keys) > self.t - 1:
node.keys.append(parent.keys[i])
parent.keys[i] = parent.children[i + 1].keys.pop(0)
if len(parent.children[i + 1].children) > 0:
node.children.append(
parent.children[i + 1].children.pop(0))
else:
parent.children[i - 1].keys.append(parent.keys.pop(i - 1))
parent.children[i - 1].keys.extend(node.keys)
parent.children.pop(i)
def _find_successor(self, node):
if node.is_leaf:
return node
else:
return self._find_successor(node.children[0])
전체 코드
import bisect
class BTreeNode:
def __init__(self, keys, children, is_leaf):
self.keys = keys
self.children = children
self.is_leaf = is_leaf
class BTree:
def __init__(self, t):
self.root = BTreeNode([], [], True)
self.t = t
def search(self, key):
return self._search_key(key, self.root)
def _search_key(self, key, node):
# get binary search lower bound index
# if current node has key, return
# if current node doesn't have key and is leaf node, return False
# if current node isn't leaf node, call recursive for child[lower_bound]
i = bisect.bisect_left(node.keys, key)
if i < len(node.keys) and key == node.keys[i]:
return (node, i)
elif node.is_leaf:
return None
else:
return self._search_key(key, node.children[i])
def insert(self, key):
# if root node is full, make root node as child
# split new root as child -> new root would get value(median) from old root
# call insert routine from root to leaf node recursively
if len(self.root.keys) == 2 * self.t - 1: # root is full
self.root = BTreeNode([], [self.root], False)
self._split_child(self.root, 0)
self._insert_key(key, self.root)
def _insert_key(self, key, node):
# get lower bound idx -> keys[i] > key
# if current node is leaf, then insert key at idx
# else, check ith child is full. if is, do split ith child
# after split ith child, ith child's median value added in cur node key
# check value and change lower bound idx for key
# call insert routine to ith child
i = bisect.bisect_left(node.keys, key)
if node.is_leaf:
node.keys.insert(i, key)
else:
if len(node.children[i].keys) == 2 * self.t - 1:
self._split_child(node, i)
if key > node.keys[i]:
i = i + 1
self._insert_key(key, node.children[i])
def _split_child(self, node, i):
# get ith child from node
# split key and child half, except median value
# get median value and insert in node
# change ith child to left part(cause smaller then median)
# insert left in i + 1 idx (case bigger than median)
c = node.children[i]
c_l = BTreeNode(c.keys[0:self.t - 1], c.children[0:self.t], c.is_leaf)
c_r = BTreeNode(c.keys[self.t:2 * self.t - 1],
c.children[self.t:2 * self.t], c.is_leaf)
median = c.keys[self.t - 1]
node.keys.insert(i, median)
node.children[i] = c_l
node.children.insert(i + 1, c_r)
def delete(self, key):
# if root key cnt is 1 and all child's node key count also t - 1
# B-Tree would shrink to h - 1
# so, before delete operation, root needs to be preprocessed
if len(self.root.keys) == 1:
root = self.root
t = self.t
left, right = root.children[0], root.children[1]
if len(left.keys) == t - 1 and len(right.keys) == t - 1:
self.root = BTreeNode([], [], False)
self.root.keys.extend(left.keys)
self.root.keys.extend(root.keys)
self.root.keys.extend(right.keys)
self.root.children.extend(left.children)
self.root.children.extend(right.children)
if len(self.root.children) == 0:
self.root.is_leaf = True
self._delete_key(key, self.root)
def _delete_key(self, key, node):
i = bisect.bisect_left(node.keys, key)
# if key matched from currnet node
if i < len(node.keys) and node.keys[i] == key:
if node.is_leaf:
node.keys.pop(i)
return
else:
successor = self._find_successor(node.children[i + 1])
node.keys[i], successor.keys[0] = successor.keys[0], node.keys[i]
self._delete_key(key, node.children[i + 1])
# if key didn't matched then check next node status
else:
if len(node.children[i].keys) == self.t - 1:
self._delete_balancing(node.children[i], node, i)
i = bisect.bisect_left(node.keys, key)
self._delete_key(key, node.children[i])
def _delete_balancing(self, node, parent, i):
# if next destination index is last pos
# next dst just has left siblings
if i == len(parent.children) - 1:
if len(parent.children[i - 1].keys) > self.t - 1:
node.keys.insert(0, parent.keys.pop())
parent.keys.append(parent.children[i - 1].keys.pop())
if len(parent.children[i - 1].children) > 0:
node.children.insert(
0, parent.children[i - 1].children.pop())
else:
parent.children[i - 1].keys.append(parent.keys.pop())
parent.children[i - 1].keys.extend(node.keys)
parent.children.pop()
# if next destination index is first pos
# next dst just has right siblings
elif i == 0:
if len(parent.children[i + 1].keys) > self.t - 1:
node.keys.append(parent.keys.pop(0))
parent.keys.insert(0, parent.children[i + 1].keys.pop(0))
if len(parent.children[i + 1].children) > 0:
node.children.append(
parent.children[i + 1].children.pop(0))
else:
parent.children[i + 1].keys.insert(0, parent.keys.pop(0))
for k in node.keys:
parent.children[i + 1].keys.insert(0, k)
parent.children.pop(0)
else:
if len(parent.children[i - 1].keys) > self.t - 1:
node.keys.insert(0, parent.keys[i])
parent.keys[i] = parent.children[i - 1].keys.pop()
if len(parent.children[i - 1].children) > 0:
node.children.insert(
0, parent.children[i - 1].children.pop())
elif len(parent.children[i + 1].keys) > self.t - 1:
node.keys.append(parent.keys[i])
parent.keys[i] = parent.children[i + 1].keys.pop(0)
if len(parent.children[i + 1].children) > 0:
node.children.append(
parent.children[i + 1].children.pop(0))
else:
parent.children[i - 1].keys.append(parent.keys.pop(i - 1))
parent.children[i - 1].keys.extend(node.keys)
parent.children.pop(i)
def _find_successor(self, node):
if node.is_leaf:
return node
else:
return self._find_successor(node.children[0])
# Print the tree
def print_tree(self, node, l=0):
print("Level ", l, " ", end=":")
for i in node.keys:
print(i, end=" ")
print()
l += 1
if len(node.children) > 0:
for i in node.children:
self.print_tree(i, l)
def main():
B = BTree(2)
for i in [10, 20, 30, 40, 50, 60, 70, 80, 90]:
B.insert(i)
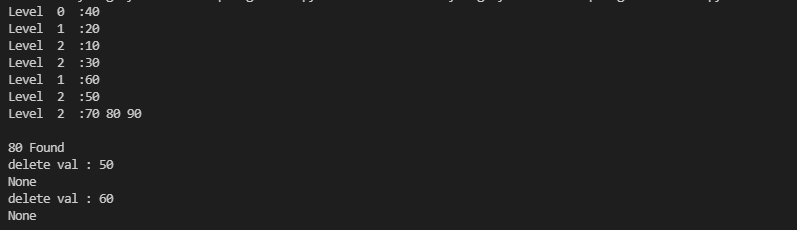
B.print_tree(B.root)
if B.search(80) is not None:
print("\n80 Found")
else:
print("\n80 Not found")
for val in [50, 60]:
print(f'delete val : {val}')
B.delete(val)
print(B.search(val))
if __name__ == '__main__':
main()