읽기 전
- 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
- 개인적으로 배운 점을 정리한 글입니다.
이진탐색트리(Binary Search Tree)란?
이진 트리의 일정으로 특정 노드의 값에 대해 왼쪽 서브트리 노드들의 값은 항상 그보다 작고 오른쪽 서브트리 노드들의 값은 항상 크게끔 배치된 트리이다. 즉, 어떤 값을 찾을 때 탐색하는 노드 대상으로 대소비교를 한 뒤 크면 오른쪽만, 작으면 왼쪽만 탐색하면 된다. 따라서 탐색 과정의 시간복잡도는 일반적인 경우 $O(log\ n)$이다.
운이 나쁜 경우
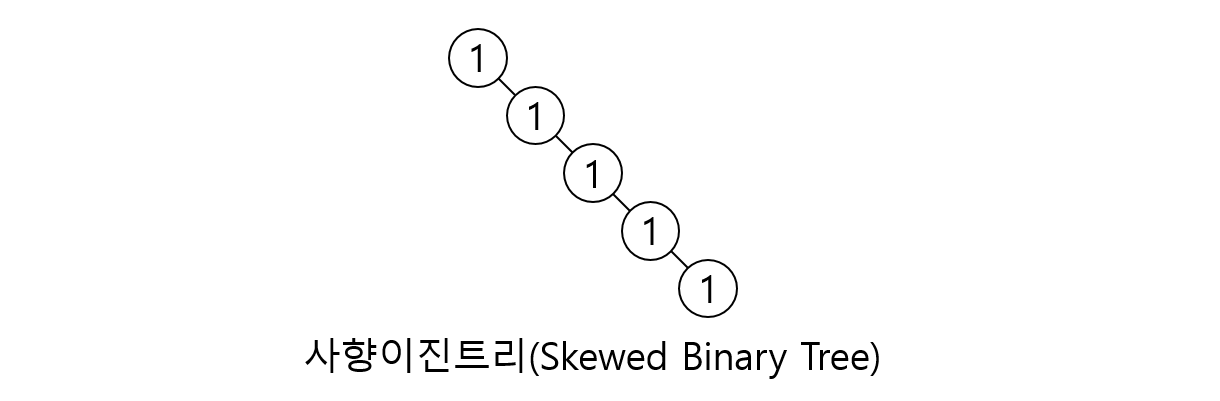
이진 탐색 트리에 1 ~ 100을 차례대로 넣으면 사향 이진트리를 만들면서 탐색 시 최대 $O(n)$의 시간이 소요될 수 있다.
일반적인 경우
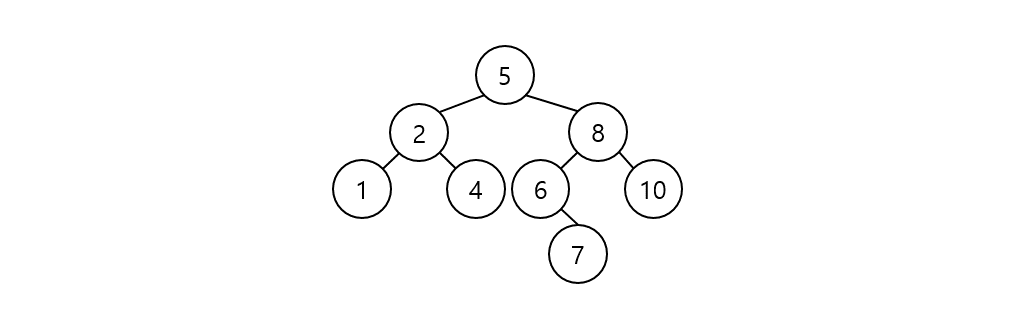
이진트리의 균형이 적절하다면 이분 탐색과 다를 바가 없으므로 시간복잡도는 $O(log\ n)$이다.
이진탐색트리(BST) 구현하기
BST 선언
class TreeNode:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
class BinarySearchTree:
def __init__(self, val):
self.root = TreeNode(val)BST 내 값 탐색
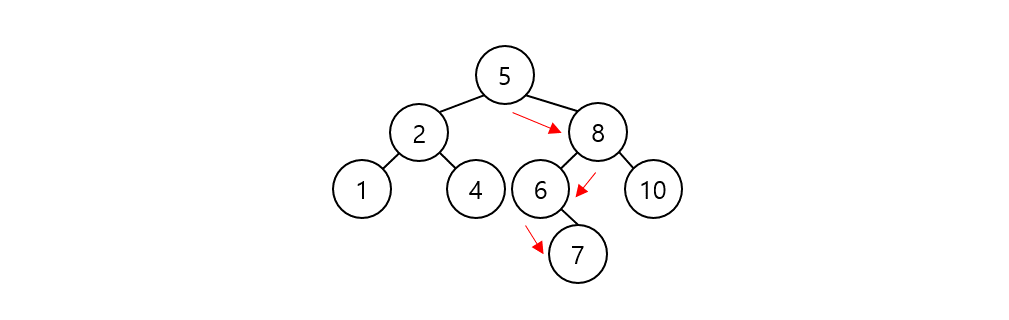
위의 BST에서 7을 찾고자 하면 5 < 7이므로 왼쪽 서브트리는 탐색할 필요가 없다. 다음 단계에서는 7 < 8이므로 우측 서브트리를 탐색할 필요가 없으며 6 < 7이므로 우측 탐색을 진행하면 원하는 값을 찾을 수 있다. 위 트리처럼 전체 크기가 8인데 총 3번만에 값을 찾게되어 log 시간 내로 결과를 받는다.
즉, 최악의 경우라도 마지막 리프 노드까지 탐색하기 때문에 트리의 높이가 $h$라 하면 탐색의 시간복잡도는 $O(h)$이라 표현할 수도 있다. 만약 마지막 리프 노드까지 진행했음에도 찾을 수 없으면 False를 반환하고 종료하면 된다.
def find(self, val):
if self.find_node(self.root, val):
return True # 노드를 반환 받으면 True
else:
return False # 없으면 False
def _find_node(self, cur, val):
if not cur:
return False # 마지막 리프노드까지 탐색해도 없으니 False
if cur.val == val:
return cur # 값을 발견하면 노드 반환
if cur.val > val: # 커서의 값이 더 크면 좌측 탐색
return self.find_node(cur.left, val)
if cur.val < val: # 커서의 값이 더 작으면 우측 탐색
return self._find_node(cur.right, val)BST 내 값 삽입

위 트리에서 3을 삽입하고자 한다. 2, 5 사이에 3을 삽입해도 해당 노드끼리는 BST의 성질에 위배되지 않을 수 있겠지만 밑의 서브트리에 대해서는 BST의 속성을 만족하지 못할 수 있다. 따라서, BST에서의 삽입은 리프 노드에서 이루어져야 한다. 그러므로 BST의 가장 왼쪽의 리프노드는 트리 내 값들 중 최소값이고 오른쪽의 리프 노드는 트리 내 값들 중 최대값이다. 결국 리프 노드 끝까지 탐색해야 하므로 시간복잡도는 트리의 높이가 $h$라 할 때 $O(h)$가 된다.

def insert(self, val):
self._insert_Node(self.root, val)
def _insert_node(self, cur, val):
if val <= cur.val:
if cur.left:
self._insert_node(cur.left, val)
else:
cur.left = TreeNode(val)
elif val > cur.val:
if cur.right:
self._insert_node(cur.right, val)
else:
cur.right = TreeNode(val)BST내 값 삭제
리프 노드 끝에서만 변경이 발생하는 삽입과 달리 삭제는 고려할 점이 더 있다. 특정 값을 삭제하면 다른 노드들과의 대소관계를 유지해야 하는데 단순히 삭제해버리면 곤란한 경우가 있다.
case 1. 리프 노드를 삭제할 경우

3이나 7을 삭제한다고 하면 단순히 삭제해도 전체 트리에 영향을 미치지 않는다.
case 2. 자식 노드가 1개인 경우

4나 6을 삭제한다고 하자. 아래에 자식 노드로 각각 3, 7을 갖고 있는데 각각에 대해 삭제하고자 하는 노드의 부모 노드에 대해 대소 관계가 유지된다. 따라서, 노드를 삭제하고 삭제된 노드의 부모노드와 삭제된 노드의 자식 노드를 연결해도 BST의 속성이 유지된다.
case 3. 자식 노드가 2개인 경우
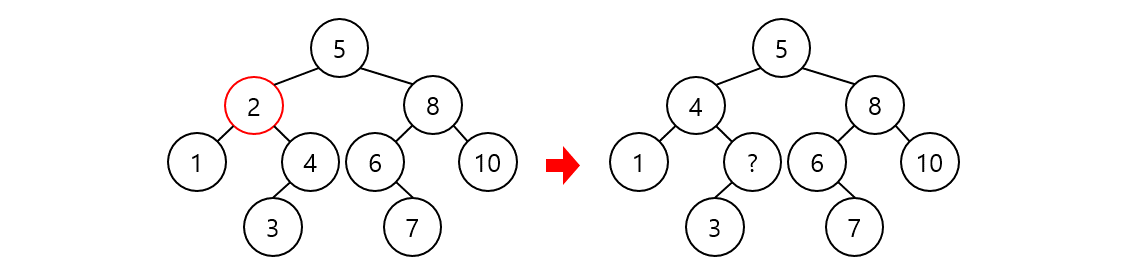
2를 삭제한다고 하자. 2를 지우고 4를 올리자니 3의 위치를 특정하기 어렵다. 별도의 방법을 사용해서 트리를 재구성할 필요가 있다. 다만, 시간복잡도를 고려해야 하므로 최대한 변경없는 방법을 써야 한다.
트리를 중위 탐색한 결과는 [1, 2, 3, 4, 5, 6, 7, 8, 10]이 될 것이다. 2를 삭제하고자 할 때 1은 predecessor(삭제 노드의 좌측 서브트리 중 최대값), 3은 successor(삭제 노드의 우측 서브트리 중 최소값)다. 만약 1이나 3을 적절히 이동시킬 수 있다면 BST의 성질을 꺠뜨리지 않고 삭제할 수 있을 것 같다. 1을 옮기면 [
1, ,1, 3, 4, 5, 6, 7, 8, 10]이 되고 3을 옮기면 [1, 3,3, 4, 5, 6, 7, 8, 10]이 된다.
predecessor나 successor의 경우 각 서브트리의 최대값 or 최소값이기 때문에 자식 노드의 개수는 0이거나 1일 수밖에 없다. 따라서, predecessor나 successor를 삭제해서 옮기는 과정은 위의 case 1이나 case 2에 해당한다.
predecessor를 옮기는 경우
- 삭제 노드의 좌측 트리를 찾는다
- predecessor(좌측 서브트리의 최대값) 노드를 찾는다.
- predecessor 노드의 자식 노드의 개수를 파악해서 case 1이나 case 2를 적용해 삭제한다.
- 삭제한 뒤 값을 반환하여 삭제할 노드에 값을 덮어씌운다.
def delete(self, val):
self._delete_node(self.root, val)
def _delete_node(self, cur, val):
if not cur: # 값을 찾을 수 없으므로 False
return False
elif cur == self.root and cur.val == val: # root값을 삭제할 경우
if cur.left and cur.right: #자식노드가 2개라면
pre_val = self._find_predecessor(cur.left) # 값 탐색
self._delete_node(cur, pre_val) # 해당 노드 삭제
cur.val = pre_val # 값 덮어씌움
elif cur.left or cur.right: # 자식노드가 1개라면
if cur.left:
self.root = cur.left
elif cur.right:
self.root = cur.right
else: # 자식노드가 없다면
self.root = None
elif cur.left and cur.left.val == val: # cur.left node를 삭제
if cur.left.left and cur.left.right:
pre_val = self._find_predecessor(cur.left.left)
self._delete_node(cur, pre_val)
cur.left.val = pre_val
elif cur.left.left or cur.left.right:
if cur.left.left:
cur.left = cur.left.left
elif cur.left.right:
cur.left = cur.left.right
else:
cur.left = None
elif cur.right and cur.right.val == val: # cur.right node를 삭제
if cur.right.left and cur.right.right:
pre_val = self._find_predecessor(cur.right.left)
self._delete_node(cur, pre_val)
cur.right.val = pre_val
elif cur.right.left or cur.right.right:
if cur.right.left:
cur.right = cur.right.left
elif cur.right.right:
cur.right = cur.right.right
else:
cur.right = None
elif cur.val > val: # 위의 탐색 조건을 모두 만족하지 않아 대소비교 시작
return self._delete_node(cur.left, val)
elif cur.val < val:
return self._delete_node(cur.right, val)
def _find_predecessor(self, cur):
if cur.right: # 만약 더 큰 값이 존재하면
return self._find_predecessor(cur.right) # 깊이 + 1
if not cur.right: # 더 큰 값이 없으면
return cur.val # 값 반환successor를 옮기는 경우
- 삭제 노드의 우측 트리를 찾는다
- successor(우측 서브트리의 최소값) 노드를 찾는다.
- successor 노드의 자식 노드의 개수를 파악해서 case 1이나 case 2를 적용해 삭제한다.
- 삭제한 뒤 값을 반환하여 삭제할 노드에 값을 덮어씌운다.
def delete(self, val):
self._delete_node(self.root, val)
def _delete_node(self, cur, val):
if not cur:
return False
elif cur == self.root and cur.val == val:
if cur.left and cur.right:
pre_val = self._find_successor(cur.right)
self._delete_node(cur, pre_val)
cur.val = pre_val
elif cur.left or cur.right:
if cur.left:
self.root = cur.left
elif cur.right:
self.root = cur.right
else:
self.root = None
elif cur.left and cur.left.val == val:
if cur.left.left and cur.left.right:
pre_val = self._find_successor(cur.left.right)
self._delete_node(cur, pre_val)
cur.left.val = pre_val
elif cur.left.left or cur.left.right:
if cur.left.left:
cur.left = cur.left.left
elif cur.left.right:
cur.left = cur.left.right
else:
cur.left = None
elif cur.right and cur.right.val == val:
if cur.right.left and cur.right.right:
pre_val = self._find_successor(cur.right.right)
self._delete_node(cur, pre_val)
cur.right.val = pre_val
elif cur.right.left or cur.right.right:
if cur.right.left:
cur.right = cur.right.left
elif cur.right.right:
cur.right = cur.right.right
else:
cur.right = None
elif cur.val > val:
return self._delete_node(cur.left, val)
elif cur.val < val:
return self._delete_node(cur.right, val)
def _find_successor(self, cur):
if cur.left:
return self._find_successor(cur.left)
if not cur.left:
return cur.val전체 코드
class TreeNode:
def __init__(self, val, left=None, right=None):
self.val = val
self.left = left
self.right = right
class BinarySearchTree:
def __init__(self, val):
self.root = TreeNode(val)
def find(self, val):
if self._find_node(self.root, val):
return True
else:
return False
def _find_node(self, cur, val):
if not cur:
return False
if cur.val == val:
return cur
if cur.val > val:
return self._find_node(cur.left, val)
if cur.val < val:
return self._find_node(cur.right, val)
def insert(self, val):
self._insert_node(self.root, val)
def _insert_node(self, cur, val):
if cur.val <= val:
if cur.right:
self._insert_node(cur.right, val)
else:
cur.right = TreeNode(val)
elif cur.val > val:
if cur.left:
self._insert_node(cur.left, val)
else:
cur.left = TreeNode(val)
def delete(self, val):
self._delete_node(self.root, val)
def _delete_node(self, cur, val):
if not cur:
return False
elif cur == self.root and cur.val == val:
if cur.left and cur.right:
pre_val = self._find_predecessor(cur.left)
self._delete_node(cur, pre_val)
cur.val = pre_val
elif cur.left or cur.right:
if cur.left:
self.root = cur.left
elif cur.right:
self.root = cur.right
else:
self.root = None
elif cur.left and cur.left.val == val:
if cur.left.left and cur.left.right:
pre_val = self._find_predecessor(cur.left.left)
self._delete_node(cur, pre_val)
cur.left.val = pre_val
elif cur.left.left or cur.left.right:
if cur.left.left:
cur.left = cur.left.left
elif cur.left.right:
cur.left = cur.left.right
else:
cur.left = None
elif cur.right and cur.right.val == val:
if cur.right.left and cur.right.right:
pre_val = self._find_predecessor(cur.right.left)
self._delete_node(cur, pre_val)
cur.right.val = pre_val
elif cur.right.left or cur.right.right:
if cur.right.left:
cur.right = cur.right.left
elif cur.right.right:
cur.right = cur.right.right
else:
cur.right = None
elif cur.val > val:
return self._delete_node(cur.left, val)
elif cur.val < val:
return self._delete_node(cur.right, val)
def _find_predecessor(self, cur):
if cur.right:
return self._find_predecessor(cur.right)
if not cur.right:
return cur.val
def _find_successor(self, cur):
if cur.left:
return self._find_successor(cur.left)
if not cur.left:
return cur.val
def print_tree(self):
return self._traverse_node(self.root, [])
def _traverse_node(self, cur, result):
if cur:
self._traverse_node(cur.left, result)
result.append(cur.val)
self._traverse_node(cur.right, result)
return result
bst = BinarySearchTree(5)
bst.insert(2)
bst.insert(3)
bst.insert(8)
bst.insert(1)
bst.insert(4)
bst.insert(6)
bst.insert(10)
bst.insert(7)
print(bst.print_tree())
print(bst.find(8))
bst.delete(8)
print(bst.find(8))
print(bst.print_tree())
bst.delete(6)
print(bst.print_tree())
bst.delete(10)
print(bst.print_tree())
bst.delete(5)
print(bst.print_tree())
bst.delete(7)
print(bst.print_tree())
bst.delete(4)
print(bst.print_tree())
'Algorithms > Data Structure' 카테고리의 다른 글
| 힙(Heap) (0) | 2021.07.02 |
|---|---|
| AVL 트리(Andelson-Velsky and Landis Tree) (0) | 2021.06.29 |
| 트리, 이진트리(Tree, Binray Tree) (0) | 2021.06.27 |
| 그래프(Graph) (0) | 2021.06.02 |
| 해시 테이블(Hash Table) (0) | 2021.05.30 |