읽기 전
- 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
- 개인적으로 배운 점을 정리한 글입니다.
트리(Tree)란?
회로(Cycle)이 없는 무방향 그래프를 의미한다. 재귀로 정의된 자기참조 자료구조로 서브트리(Subtree)들로 구성된다.
트리에서 사용하는 용어

- 노드(Node): 트리를 구성하는 기본 원소
- 로트 노드(Root Node / Root): 부모가 없는 최상위 노드, 트리의 시작
- 부모 노드(Parent Node): 특정 노드에 대해 루트 방향으로 직접 연결된 상위 노드
- 자식 노드(Child Node): 특정 노드에 대해 루트 반대 방향으로 직접 연결된 하위 노드
- 형제 노드(Siblings Node): 동일한 부분 노드를 갖는 노드들
- 리프 노드(Leaf Node) / 단말 노드(Terminal Node): 자식이 없는 노드
- 경로(Path): 출발 노드에서 도착 노드까지의 노드들의 순서
- 길이(Length): 출발 노드에서 도착 노드까지의 노드들의 개수
- 깊이(Depth): 출발 노드에서 루트까지의 경로 길이
- 레벨(Leval): 루트 노드부터 도착 노드까지의 간선/링크의 개수를 공유하는 노드의 그룹
- 높이(Height): 루트에서 가장 최하위 노드까지의 경로 길이
- 차수(Degree): 각 노드가 갖는 자식 노드의 개수
- 트리의 차수(Degree of tree): 트리의 각 노드들의 갖는 차수 중 최대값
- 크기(Size): 자신과 자식 노드들의 개수
- 너비(Width): 가장 많은 노드를 갖고 있는 레벨의 크기
트리의 특징
- 노드의 N개면 간선의 개수는 N - 1개다.
- 루트에서 특정 노드로 가는 경로는 유일하다. 임의의 두 노드도 마찬가지다.
- 반드시 루트 노드는 1개만 존재하며 모든 자식 노드는 한개의 부모 노드만을 갖는다.
- 트리의 순회는 Pre-Order(전위), In-Order(중위), Post-Order(후위)로 이루어진다.
이진 트리 (Binary Tree)란?
트리 중 자식 노드를 최대 2개까지만 갖는 가장 간단한 형태의 트리다. 자식 노드가 2개보다 많으면 m-ary트리(다향 트리, 다진 트리)라고 한다.
이진 트리의 종류
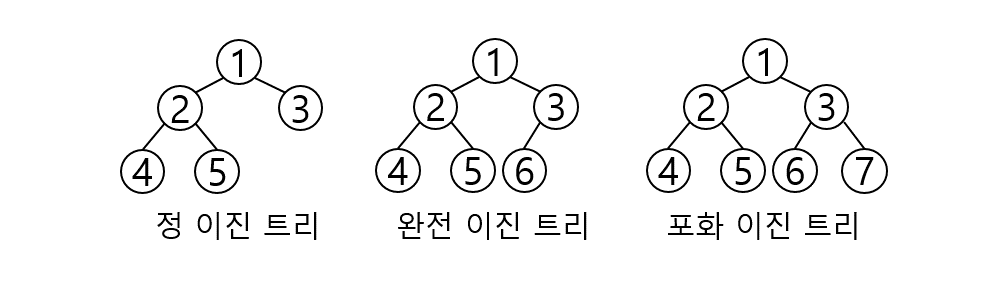
정 이진 트리(Full Binary Tree): 트리의 모든 노드들에 대해 자식 노드의 개수가 0이나 2인 이진 트리
완전 이진 트리(Complete Binary Tree): 마지막 레벨을 제외한 모든 레벨들이 완전히 채워져 있으며 마지막 레벨의 노드들은 가장 왼쪽부터 차례대로 채워진 이진 트리
포화 이진 트리(Perfect Binary Tree): 리프노드를 제외한 모든 노드가 2개의 자식 노드를 가지며 모든 리프 노드가 동일한 길이/높이를 갖는다. 즉, 트리의 높이가 n일 때 해당 트리가 가질 수 있는 노드의 개수는 최대 $2^n-1$이고 곧 포화 이진 트리가 갖는 노드의 개수이다.
트리의 구현

노드 정의하기
class TreeNode(object):
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
root = TreeNode(1)
root.left = TreeNode(2, TreeNode(4), TreeNode(5, TreeNode(8)))
root.right = TreeNode(3, TreeNode(6), TreeNode(7))트리의 순회 - 전위, 중위, 후위
트리의 순회에는 전위(Pre-Order), 중위(In-Order), 후위(Post-Order) 3가지 방식이 있다. 문제의 요구사항에 맞춰서 적절히 사용하면 된다. 주로 단순 탐색이나 다른 탐색 순서에 따른 경로가 주어지면 재조합해서 나머지 탐색 경로를 출력하는 문제에 쓰인다.
def pre_order(t:TreeNode, result:list):
if t:
result.append(t.val)
pre_order(t.left)
pre_order(t.right)
return result
def in_order(t:TreeNode, result:list):
if t:
in_order(t.left)
result.append(t.val)
in_order(t.right)
return result
def post_order(t:TreeNode, result:list):
if t:
post_order(t.left)
post_order(t.right)
result.val
return result
result = pre_order(root, [])
print(f'pre-order path: {result}')
result = pre_order(root, [])
print(f'in-order path: {result}')
result = pre_order(root, [])
print(f'post-order path: {result}')
'Algorithms > Data Structure' 카테고리의 다른 글
| AVL 트리(Andelson-Velsky and Landis Tree) (0) | 2021.06.29 |
|---|---|
| 이진탐색트리(Binary Search Tree, BST) (0) | 2021.06.28 |
| 그래프(Graph) (0) | 2021.06.02 |
| 해시 테이블(Hash Table) (0) | 2021.05.30 |
| 이중 연결리스트 - Doubly Linked List (0) | 2021.05.18 |