읽기 전
- 불필요한 코드나 잘못 작성된 내용에 대한 지적은 언제나 환영합니다.
- 개인적으로 사용해보면서 배운 점을 정리한 글입니다.
힙 정렬(Heap Sort)?
우선순위 큐 등을 위해 구현했던 힙(Heap) 자료구조를 응용한 정렬 알고리즘이다. Heap Sort에서 사용하는 힙 생성 과정은 주어진 배열을 차례대로 삽입하지 않고 전체 배열을 한번에 Heap 구조로 바꾼다는 점에서 Analysis of Algorithms | Time Complexity of building a heap의 BUILD-HEAP 함수라 할 수 있다.(길이 n인 배열의 BUILD-HEAP의 시간복잡도가 $O(n)$라는 내용)
힙 정렬 동작

위 배열을 정렬한다고 하자.
먼저 최대 힙(Max Heap) 구현을 해야한다. 최대 힙 구현은 전체 배열의 길이를 n이라 할 때 자식 노드를 갖는 마지막 부모노드가 $n\ //\ 2$ or $\lfloor \cfrac{n}{2} \rfloor$번째 노드임을 상기하면 되겠다. 그렇다면 $\lfloor \cfrac{n}{2} \rfloor$번째 노드부터 첫 번째 노드까지 heapify를 수행하면 정렬되지는 않았지만 적어도 부모 노드와 자식 노드 간의 대소 관계는 만족하는 최대 힙을 얻을 수 있다.
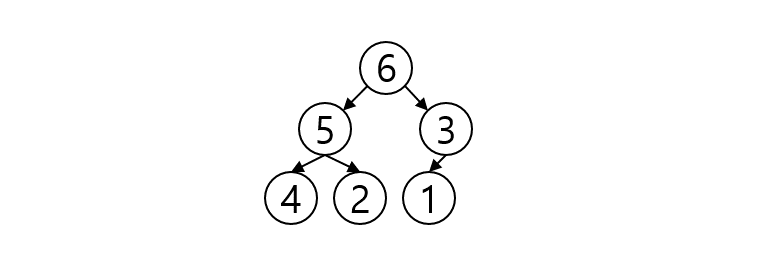
위 과정을 흔히 수도코드로 BUILD-HEAP이라 부르며 수학적으로 굳이 모든 노드에 대해 탐색할 필요가 없으므로 시간복잡도는 $O(n\log\ n)$이 아니라 $O(n)$이다. 증명 과정은 Analysis of Algorithms | Time Complexity of building a heap을 참고하면 되겠다.
최대 힙을 구현했으니 본격적으로 정렬 과정을 구현해야 한다. 최대 힙의 루트 노드가 전체 트리의 최대 값이라는 성질을 이용한다. 루트 노드는 최대값이므로 정렬하고자 하는 배열의 가장 마지막으로 보내는 작업을 반복하면 된다.
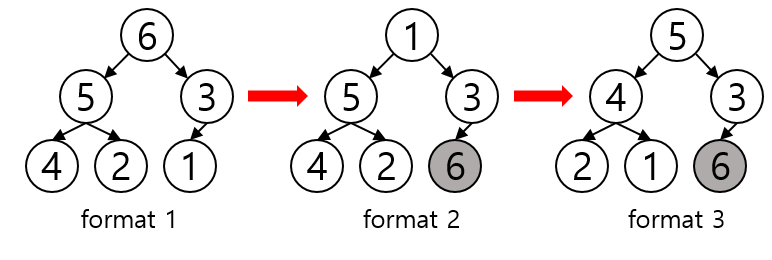
루트 노드 6을 가장 끝 원소와 swap하면 format 2가 되고 마지막 원소를 제외한 나머지 트리에 대해 heapify를 수행하면 format 3으로 바뀐다. (6 정렬 완료)

루트 노드 5를 n-1번째 위치로 swap하면 format 2가 되고 나머지 트리에 대해 heapify를 수행하면 format 3으로 바뀐다. (5, 6 정렬 완료)
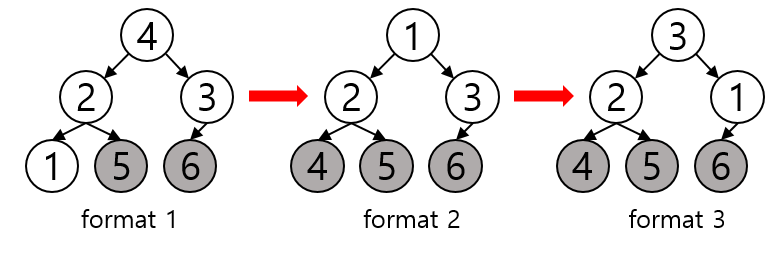
루트 노드 4를 n-2 번째 위치로 swap하면 format 2가 되고 나머지 트리에 대해 heapify를 수행하면 format 3으로 바뀐다. (4, 5, 6 정렬 완료)
위와 같이 마지막 원소부터 첫 번째 원소까지 차곡차곡 쌓여 루틴이 끝나면 의도한대로 정렬된 배열을 얻을 수 있다.
힙 정렬의 전체 시간복잡도는 처음 Max Heap을 만들기 위한 BUILD-HEAP 과정에서 tight하게 고려하여 $O(n)$라 할 지라도, 정렬 과정에서 n회 + 높이 lon\ n으로 $O(n\cdot log\ n)$이 되어 $O(nlog\ n)$이다. 공간복잡도 즉, 메모리는 재귀 호출 등으로 인한 스택 내 부분 배열의 생성 없이 swap만을 사용하여 제자리 정렬이 이루어지므로 $O(1)$이다.
python 코드
def heap(arr):
def heapify(i, l):
largest = i
left, right = i * 2 + 1, i * 2 + 2
if left < l and arr[largest] < arr[left]:
largest = left
if right < l and arr[largest] < arr[right]:
largest = right
if largest != i:
arr[i], arr[largest] = arr[largest], arr[i]
heapify(largest, l)
n = len(arr)
# BUILD-HEAP 수행, 0좌표 기반이므로 마지막 부모는 n // 2 - 1
for idx in range(n // 2 - 1, -1, -1):
heapify(idx, n)
for i in range(n - 1, 0, -1):
arr[0], arr[i] = arr[i], arr[0] # 최대값 i좌표로
heapify(0, i) # 0부터 i-1까지 heapify
return arr
'Algorithms > Algorithm' 카테고리의 다른 글
| 이진 탐색(Binary Search) 알고리즘 (0) | 2021.07.10 |
|---|---|
| 카운팅 정렬(Counting Sort, 계수 정렬) 알고리즘 (0) | 2021.07.08 |
| 퀵 정렬(Quick Sort) 알고리즘 (0) | 2021.07.08 |
| 병합 정렬(Merge Sort) 알고리즘 (0) | 2021.07.08 |
| 삽입 정렬(Insertion Sort) 알고리즘 (0) | 2021.07.07 |